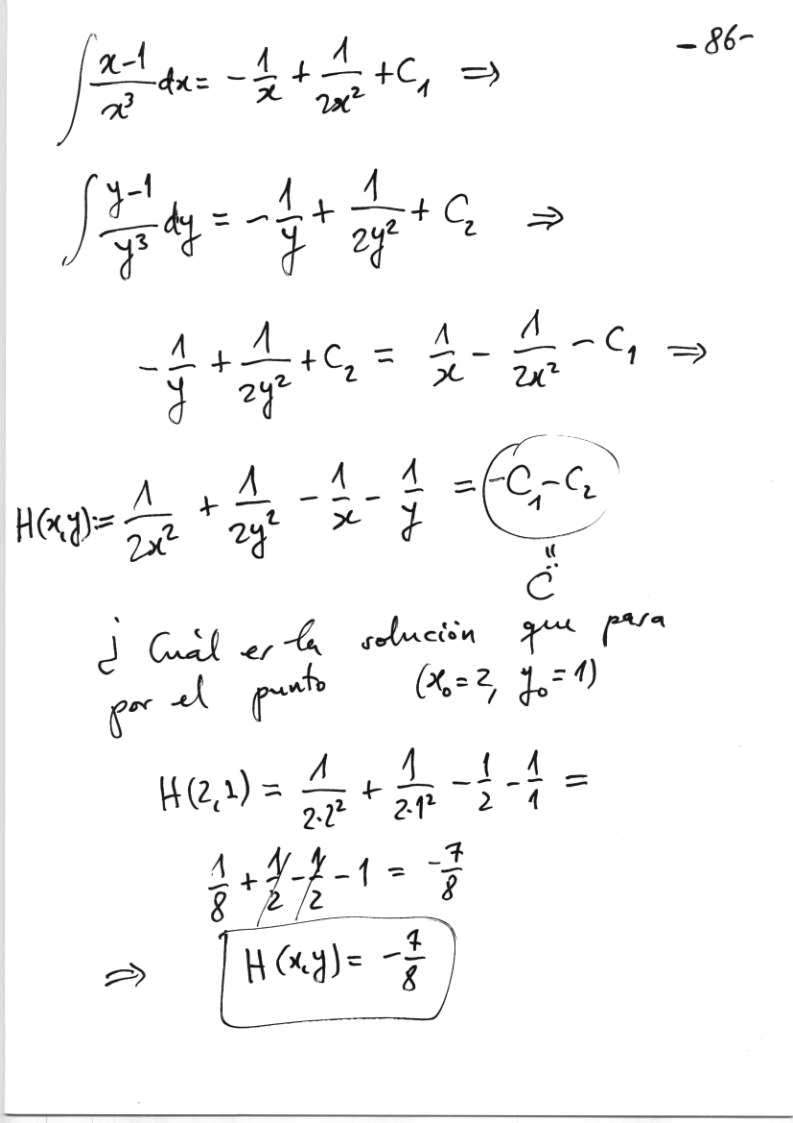Ampliación de Matemáticas. Curso actual.
Grupo 16 de 1º de Ciencias Ambientales.
Transparencias 111 a la 120.
Juan-Miguel Gracia
<=== Principio
Siguientes ===>
Transparencia 111

Transparencia 112

Transparencia 113

Transparencia 114

Transparencia 114 bis: Solución del Ejercicio 4, hoja 83.
Tema II: Ecuaciones diferenciales de primer orden integrables elementalmente
Transparencia 115

Ejemplo.- Vamos a establecer el enunciado del ejercicio que se resuelve en las hojas 85 y 86, de esta manera diferente:
Hallar la solución general de la ecuación diferencial
$\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}= \frac{(x-1)y^3}{x^3(1-y)}.} $
Después hallar la solución particular que satisface la condición $\textstyle{y(2)=1}.$
Observación.- Esta ecuación diferencial es de variables separadas
$\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}x}= f(x)\,g(y)}$,
donde
$\displaystyle{f(x)= \frac{x-1}{x^3}, \quad g(y)=\frac{y^3}{1-y}.} $
Solución.- Separando las variables queda
$\displaystyle{\frac{\mathrm{d}y}{g(y)}= f(x) \mathrm{d}x; } $
es decir,
$\displaystyle{\frac{1-y}{y^3} \mathrm{d}y= \frac{x-1}{x^3} \mathrm{d}x}. $
El método para resolver esta ecuación diferencial consiste en integrar sus dos miembros:
$\int \displaystyle{\frac{1-y}{y^3} \mathrm{d}y= \int \frac{x-1}{x^3} \mathrm{d}x}; $
Para que resulte la misma expresión que en la hoja 85, multiplicamos por $\textstyle{-1}$ los dos miembros de esta igualdad:
$\int \displaystyle{\frac{y-1}{y^3} \mathrm{d}y= -\int \frac{x-1}{x^3} \mathrm{d}x},\ldots $
Transparencia 116

Transparencia 117
Transparencia añadida
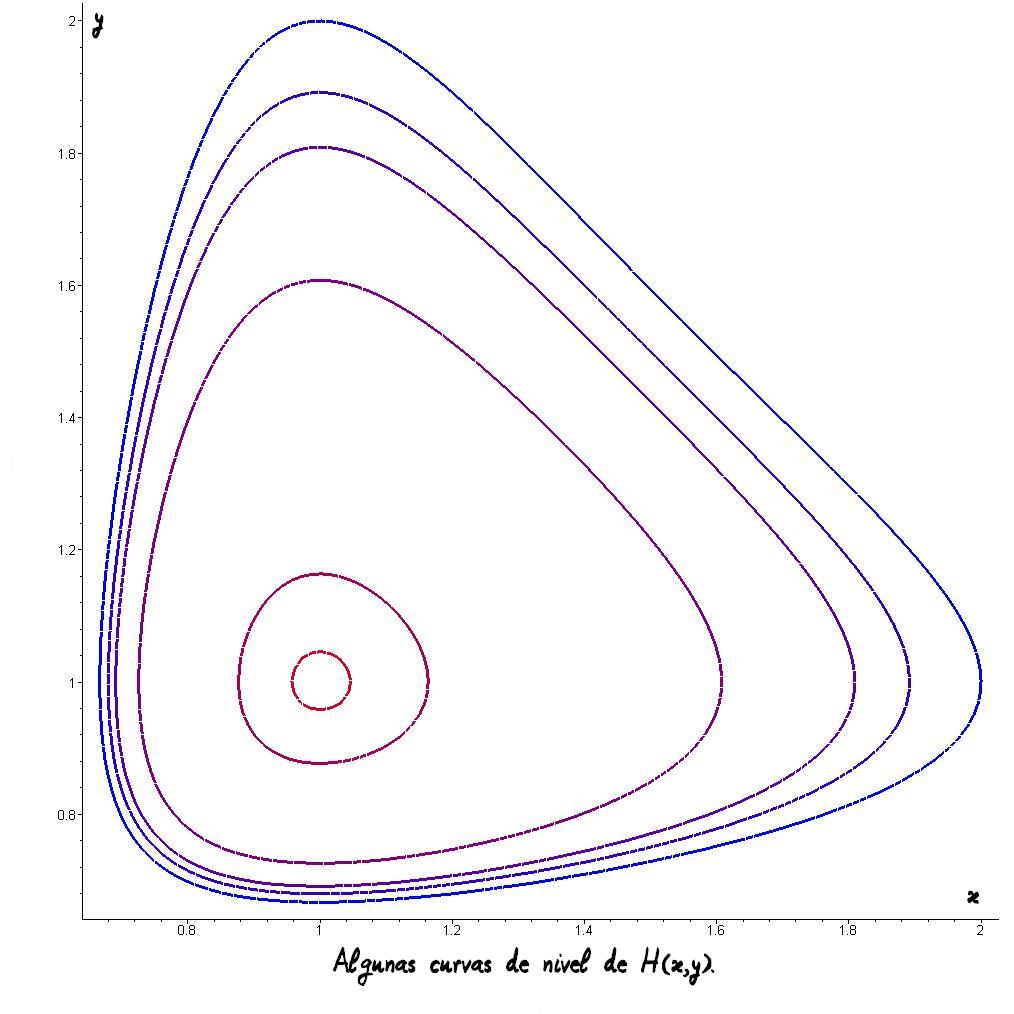
Transparencia añadida
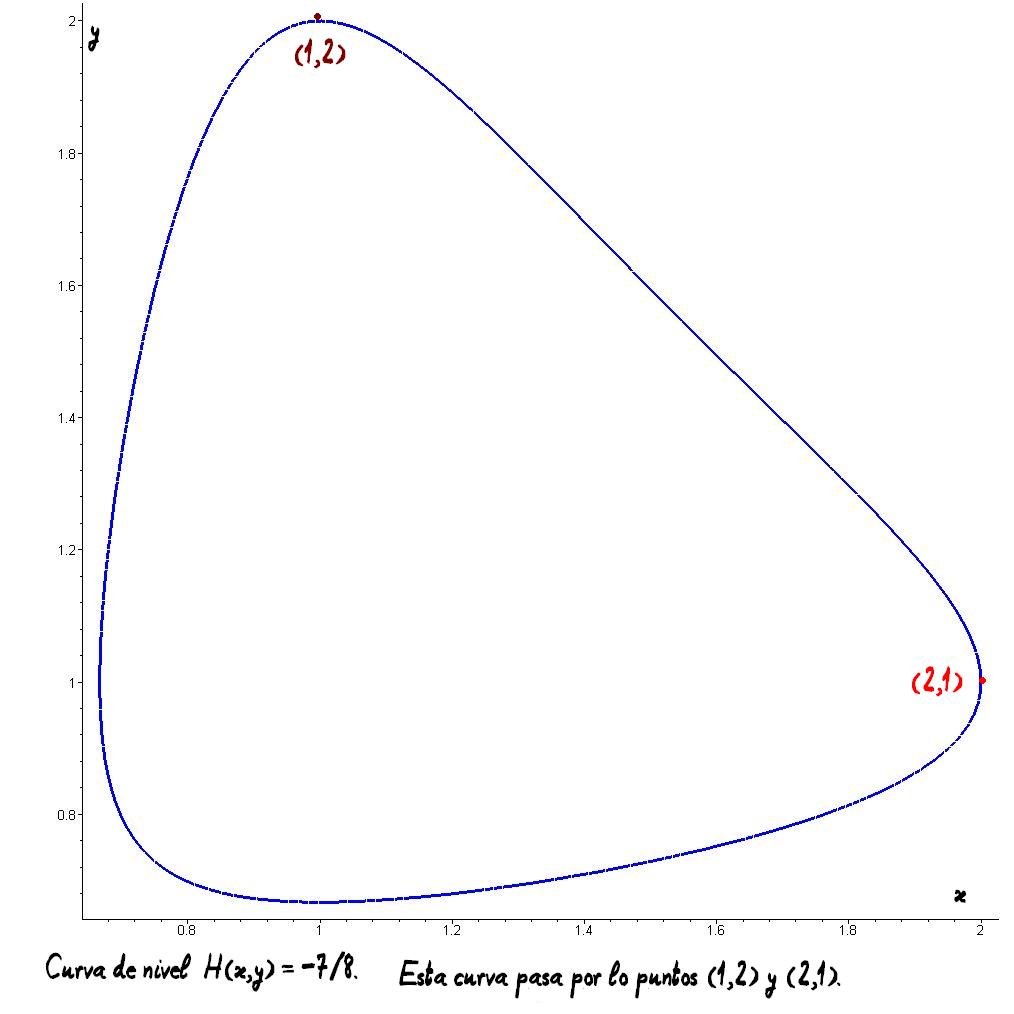
Transparencia 118

Transparencia 119
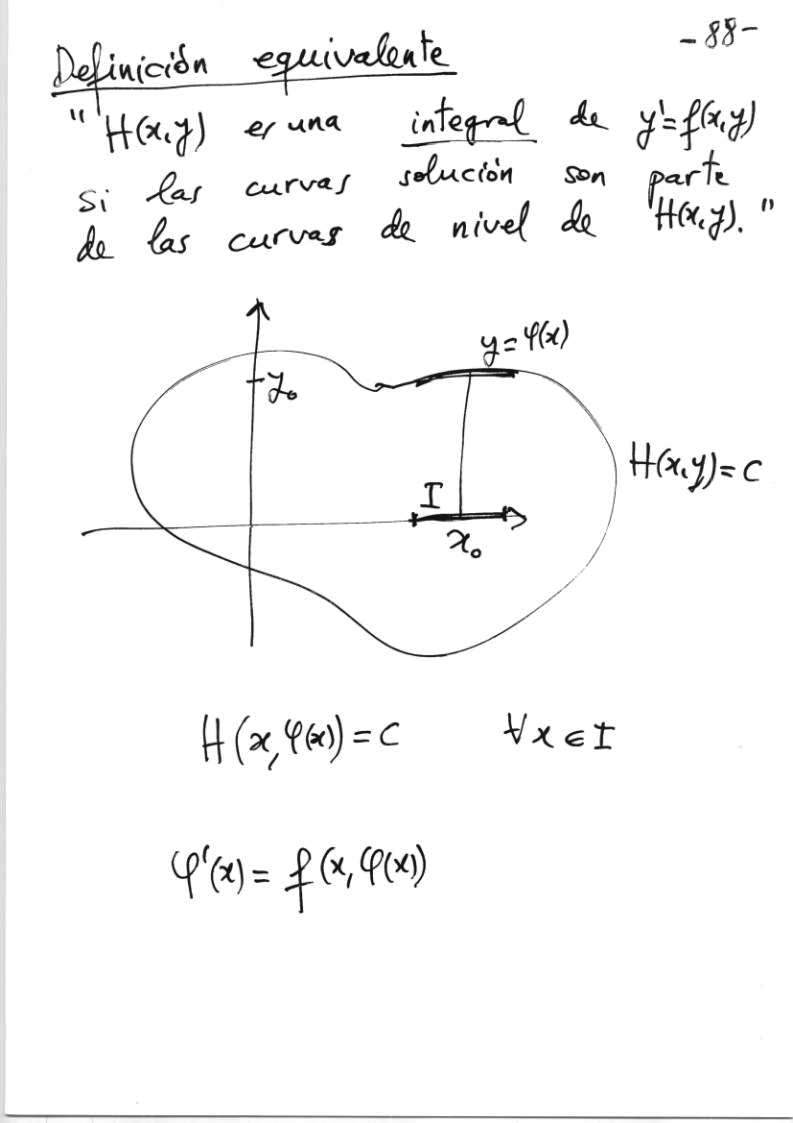
Transparencia 120

<=== Principio
Siguientes
===>
Portada
de la Sección Departamental
Modificado el 26 de abril de 2010.
Página administrada por Juan-Miguel Gracia: