Las soluciones maximales de $\textstyle{y'=x^2+y^2}$ están definidas en un intervalo finito.

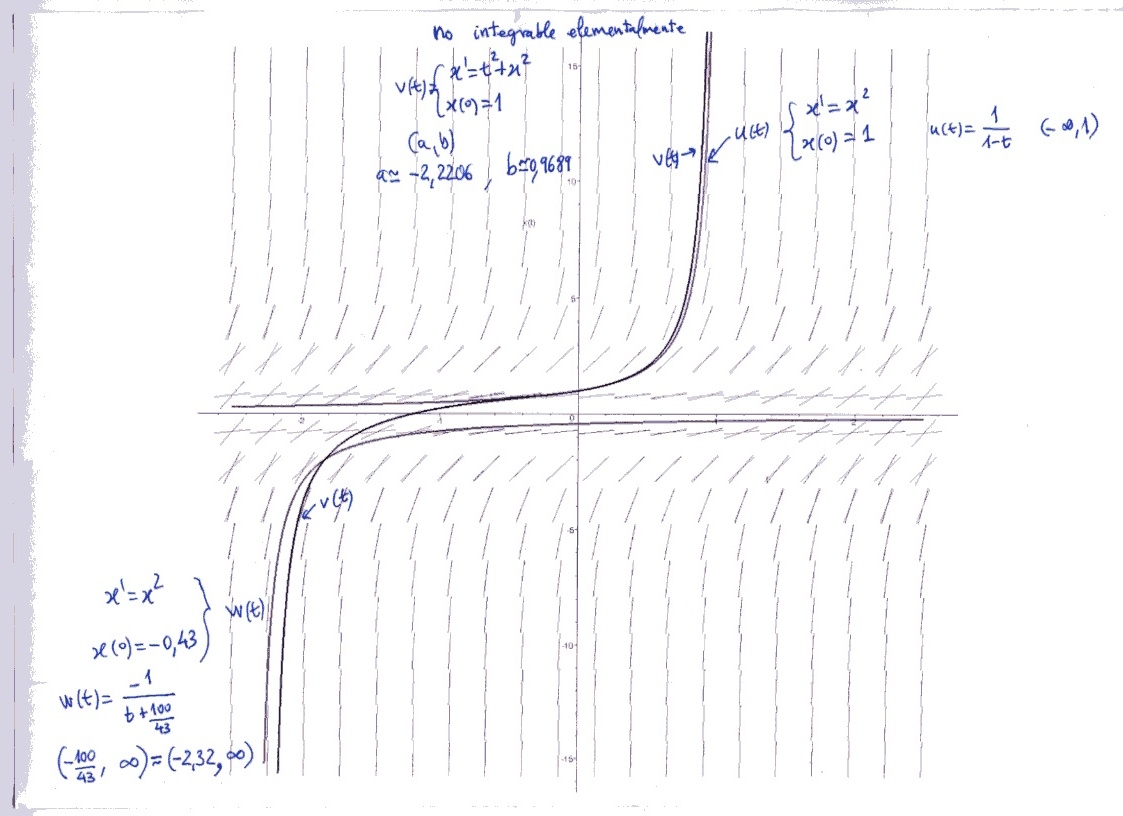
Por conveniencia denotaremos esta ecuación diferencial mediante $\textstyle{x'=t^2+x^2. }$

Según puede leerse en el prefacio del libro de Peter Henrici "Discrete variable methods for ordinary differential equations", Wiley, New York, 1962, esta ecuación diferencial no puede integrarse elementalmente. Para fijar las ideas consideraremos en primer lugar la solución maximal (o no prolongable) $\textstyle{v(t)}$ de la ecuación $\textstyle{ x'=t^2+x^2}$ que satisface la condición inicial $\textstyle{x(0)=1. }$ Llamemos $\textstyle{(a,b) }$ al intervalo abierto en el que está definida $\textstyle{v(t)}$; en principio, los extremos de este intervalo pueden ser $\textstyle{-\infty, \infty}$. Empezaremos suponiendo que $\textstyle{(a,b)=(-\infty,\infty)}$ y demostraremos por reducción al absurdo que esto no es posible. En primer lugar, demostraremos que $\textstyle{0 \lt b \lt 1}$. En segundo lugar, probaremos que $\textstyle{-100/43 \lt a \lt 0.}$

Teorema.- Las soluciones maximales de $x'=t^2+x^2$ no están definidas en toda la recta real $\mathbb R$.

Demostración.- Comenzaremos con el

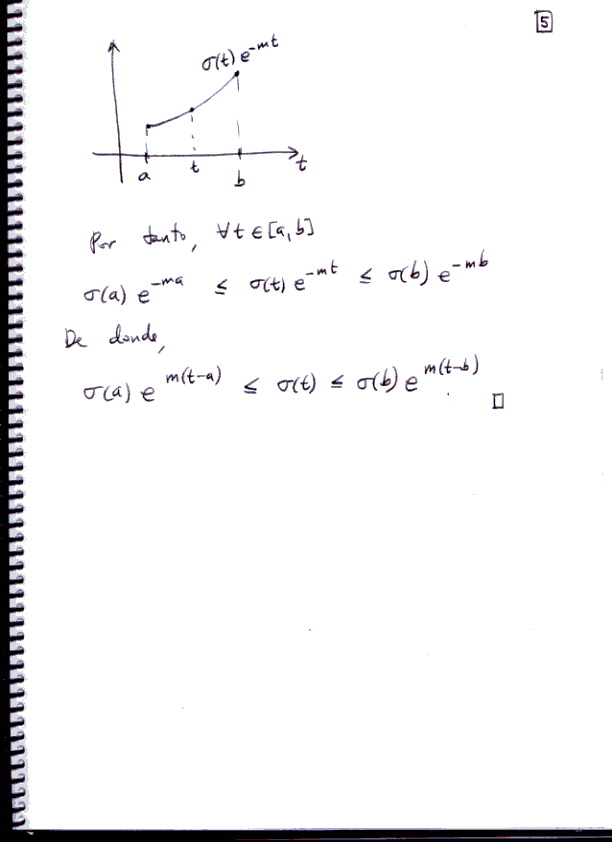
Lema 1.- Sea $\sigma(t)$ una función real derivable que satisface la desigualdad diferencial

Transparencia 1





Transparencia 2





Transparencia 3





Transparencia 4





Transparencia 5





Transparencia 6





Transparencia 7





Transparencia 8





Transparencia 9





Transparencia 10

Referencias

[1] Garret Birkhoff and Gian-Carlo Rota: Ordinary differential equations. Second edition. John Wiley, New York, 1969. Página 22: Lemma 2. Páginas 25: Theorem 7.