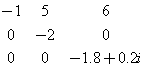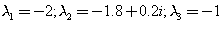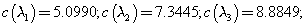Pseudoespectros de matrices.
El pseudoespectro de una matriz A compleja cuadrada de orden n de nivel
ε > 0 se define como el conjunto unión de todos los espectros de las
matrices X que distan de
A menos o igual que ε en la distancia del espacio de matrices asociada
a la norma espectral matricial. Se denota por Λε (A).
A continuación mostramos una imagen gif que describe la evolución de
Λε (A)
al crecer ε desde 0.

Esta animación corresponde a la matriz de orden 3
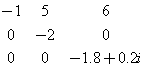
cuyos valores propios son
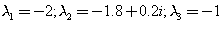
Los números de condición de estos valores propios (simples) son, respectivamente,
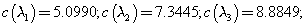
Las tres componentes conexas del pseudoespectro de nivel ε crecen
tanto más rápidamente cuanto mayor es el número de condición del valor
propio de A que contienen. De hecho si δj(ε) es el
diámetro
de la componente conexa que contiene al j-ésimo valor propio,
entonces su derivada por la derecha en 0 viene dada por
δ'j(0+)= 2 c(λj).
Más información sobre pseudoespectros
de una matriz puede verse en

Modificada el 9 de junio de 2009.
Páginas administradas por Juan-Miguel Gracia: