Ampliación de Matemáticas. Curso actual.
Grupo 16 de 1º de Ciencias Ambientales.
Transparencias 60 a la 70.
Juan-Miguel Gracia
<=== Principio Siguientes ===>
Campos de direcciones. Curvas isoclinas.
Transparencia añadida.
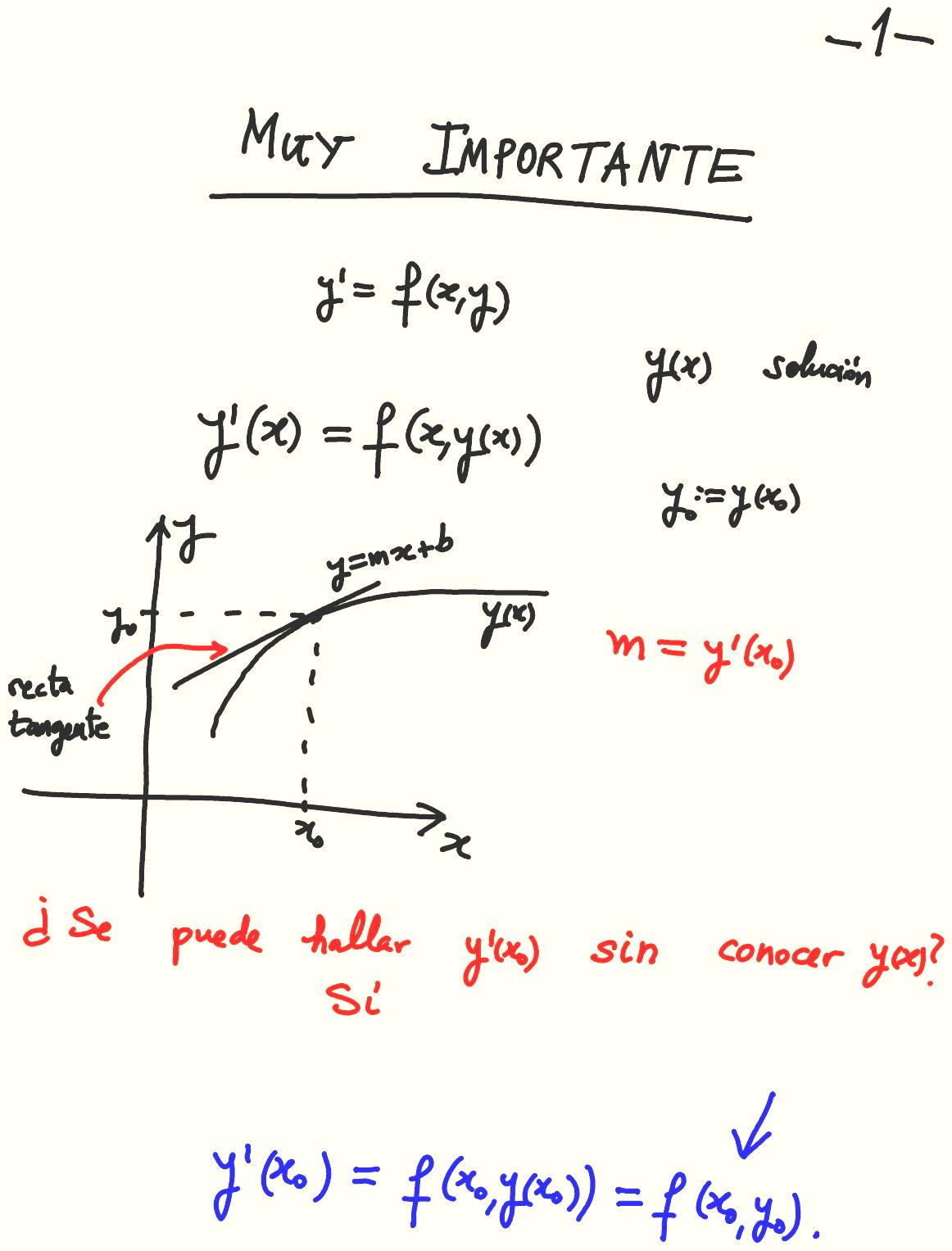
Transparencia añadida.

Transparencia añadida.
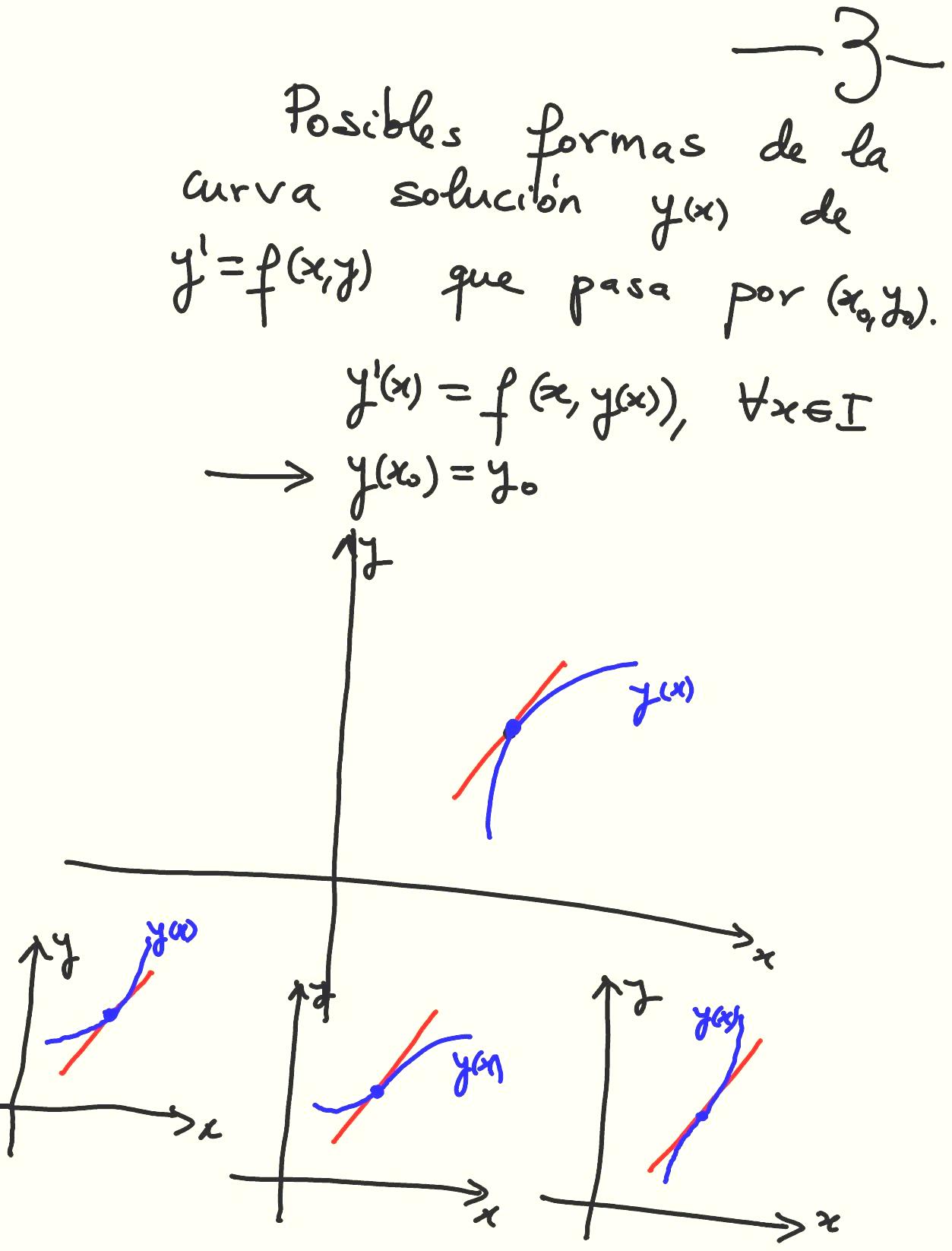
Transparencia añadida.

Transparencia añadida.
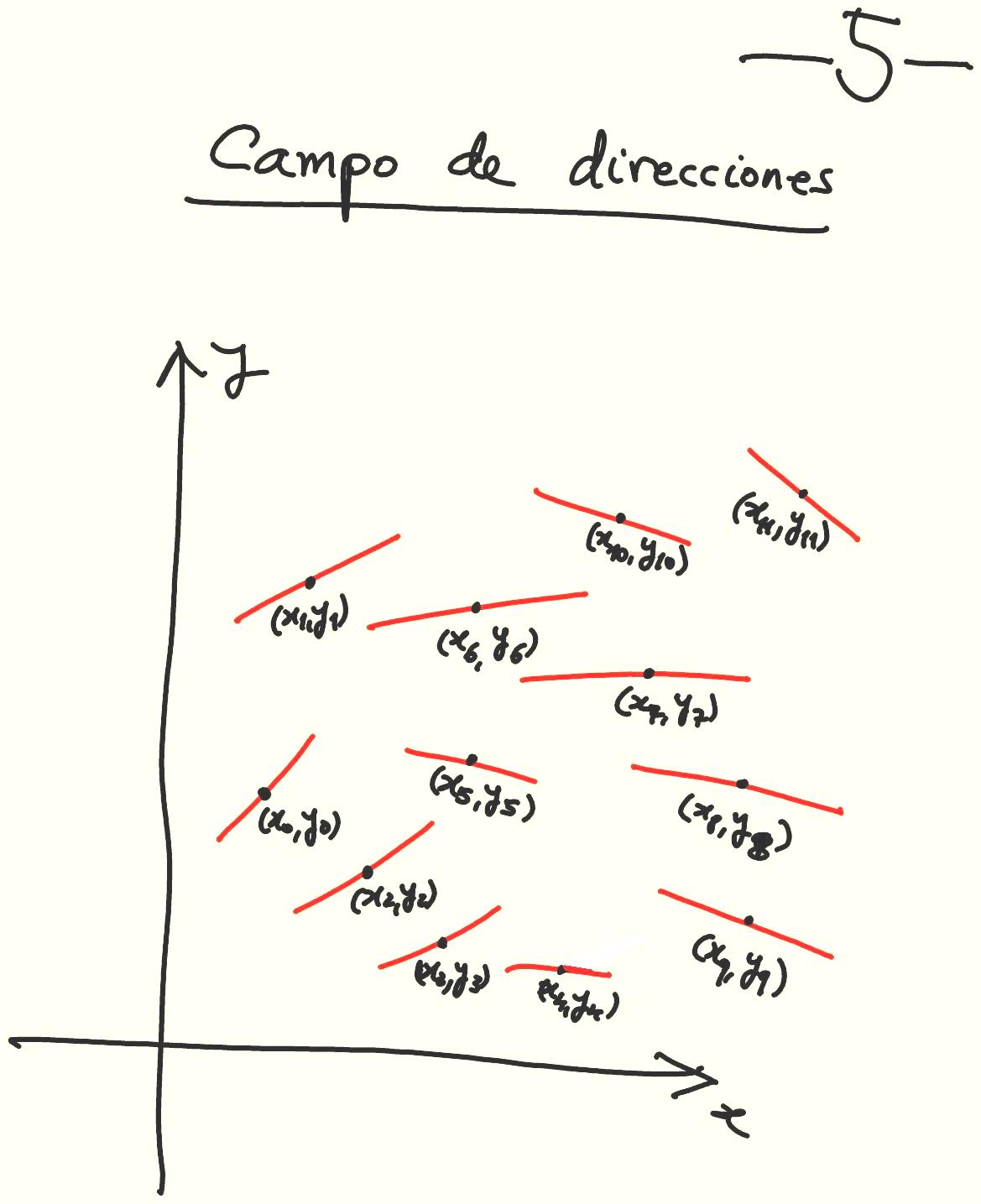
Transparencia añadida.
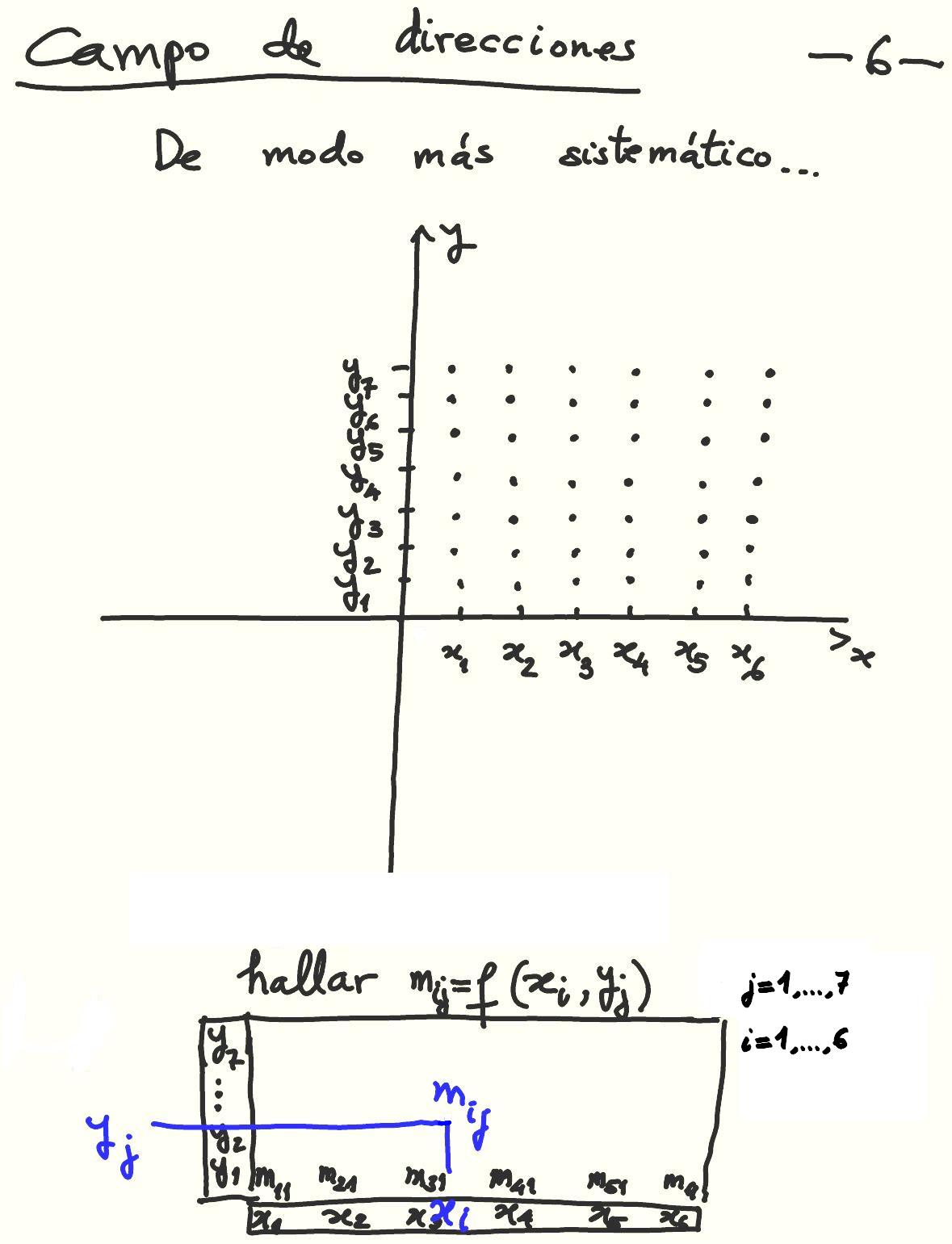
Transparencia añadida.
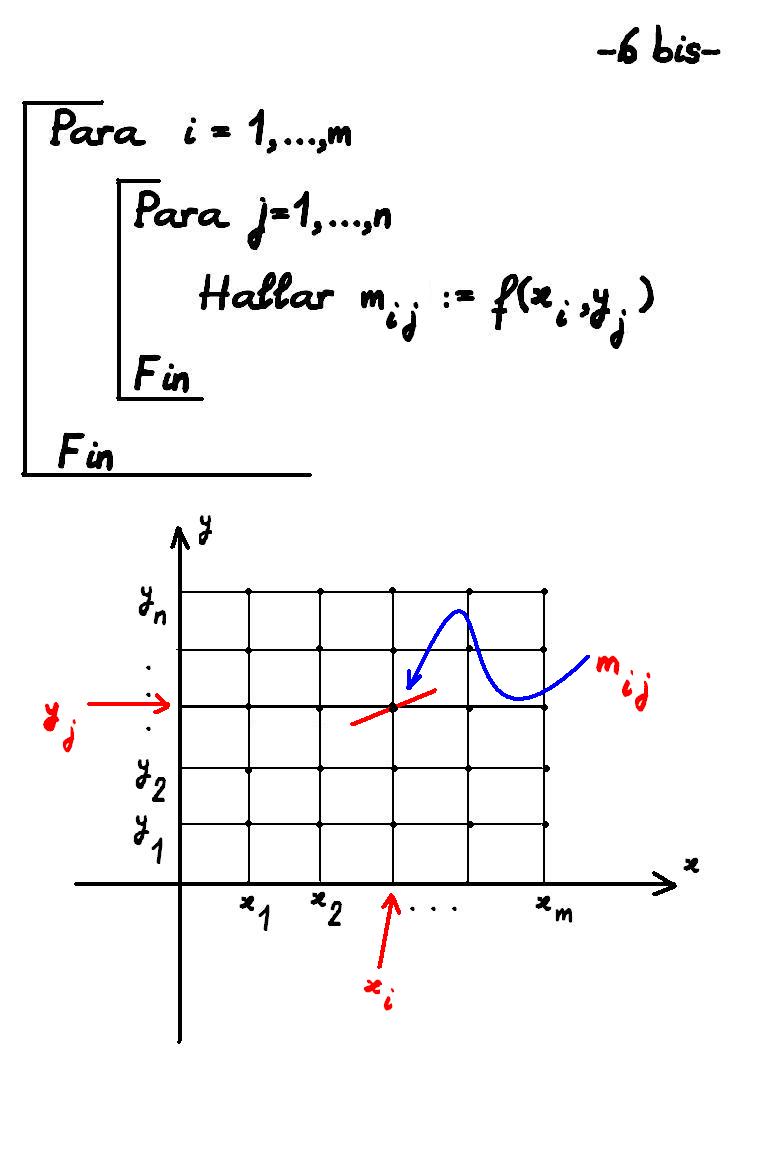
Transparencia añadida.

Transparencia 60.
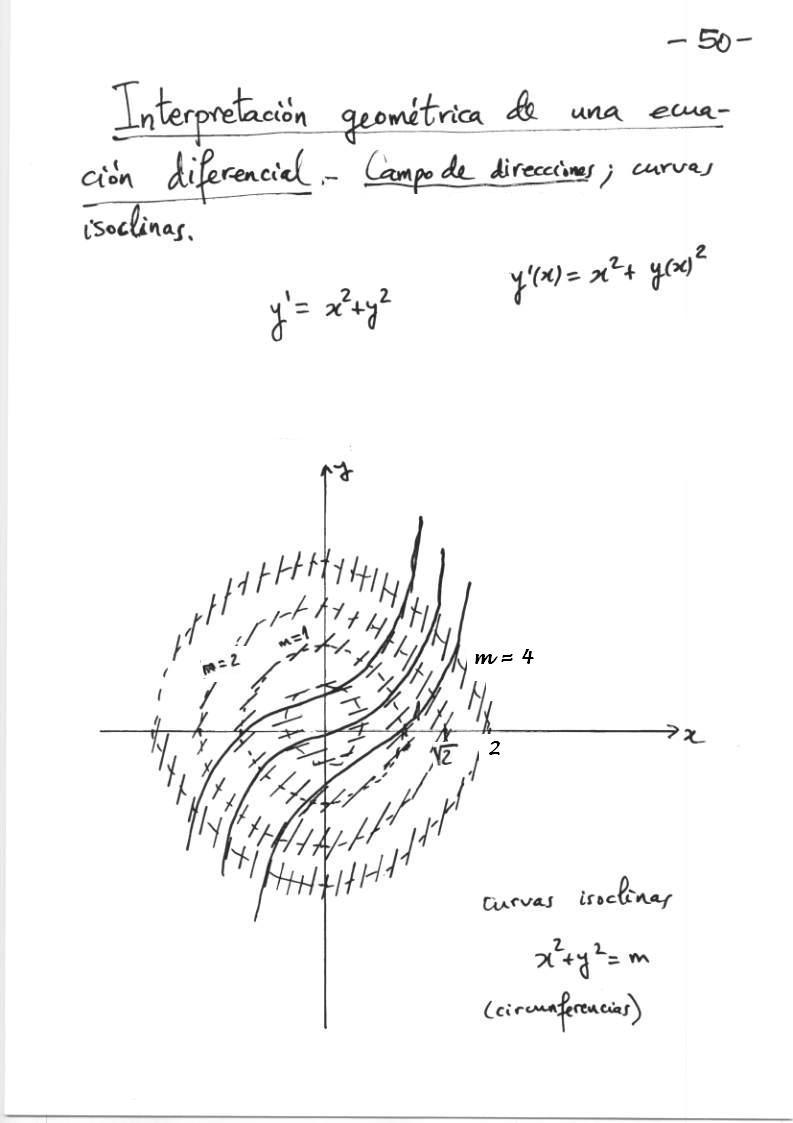
Atención: no es cierto que las
soluciones y(x) de y'=x2+y2 estén definidas para todo valor de
x . Véase una demostración de este aserto aquí.
Transparencia añadida.
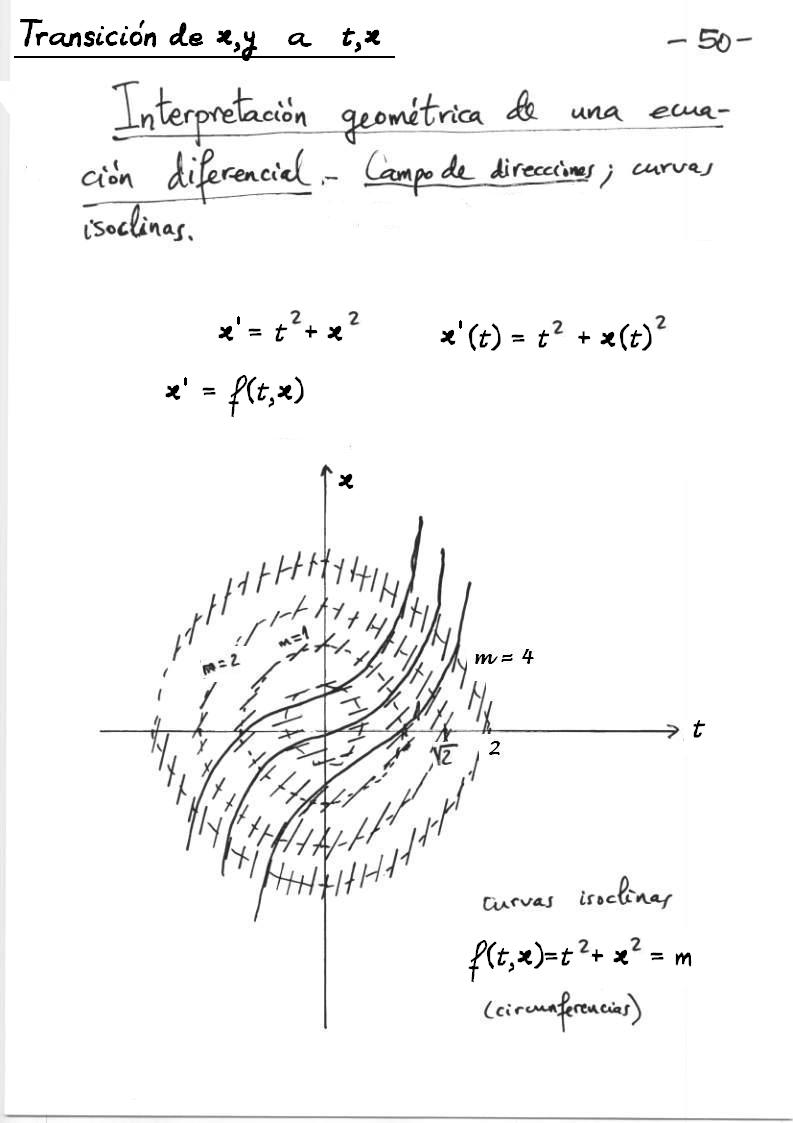
Trayectorias tangentes al campo de pendientes
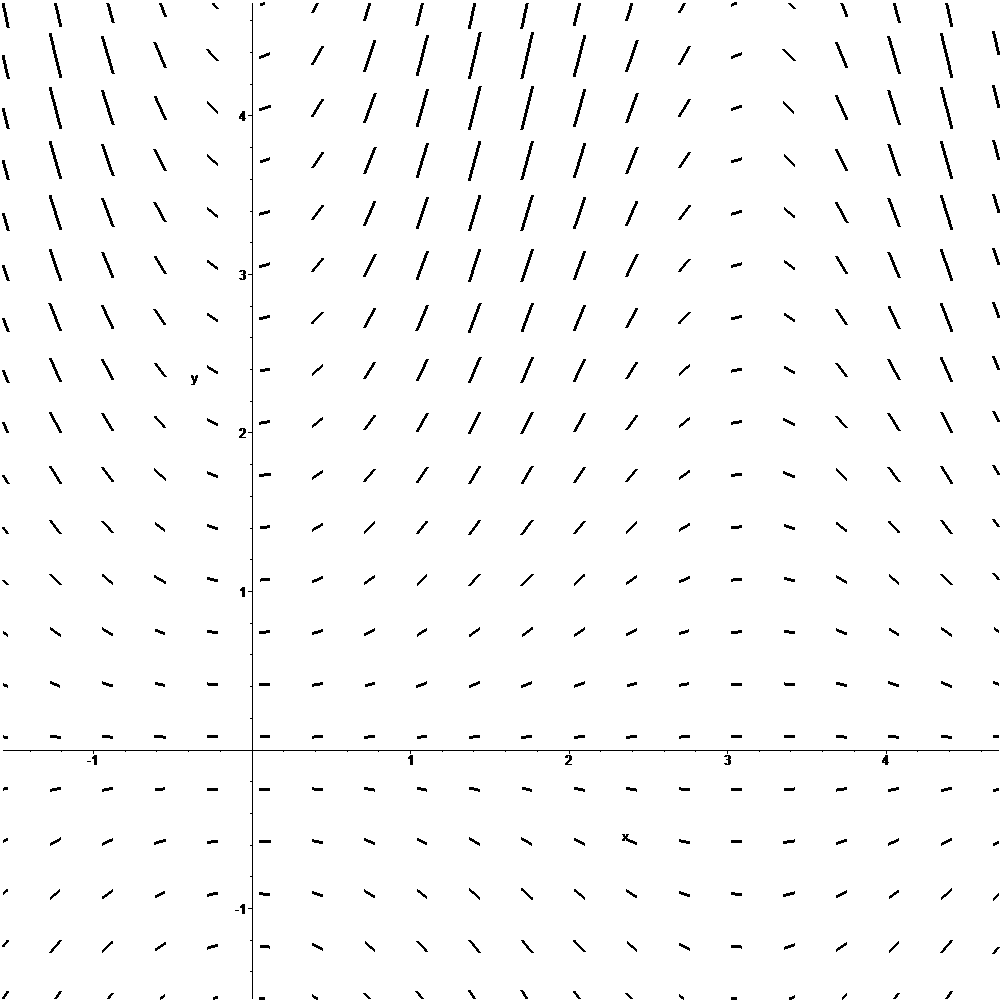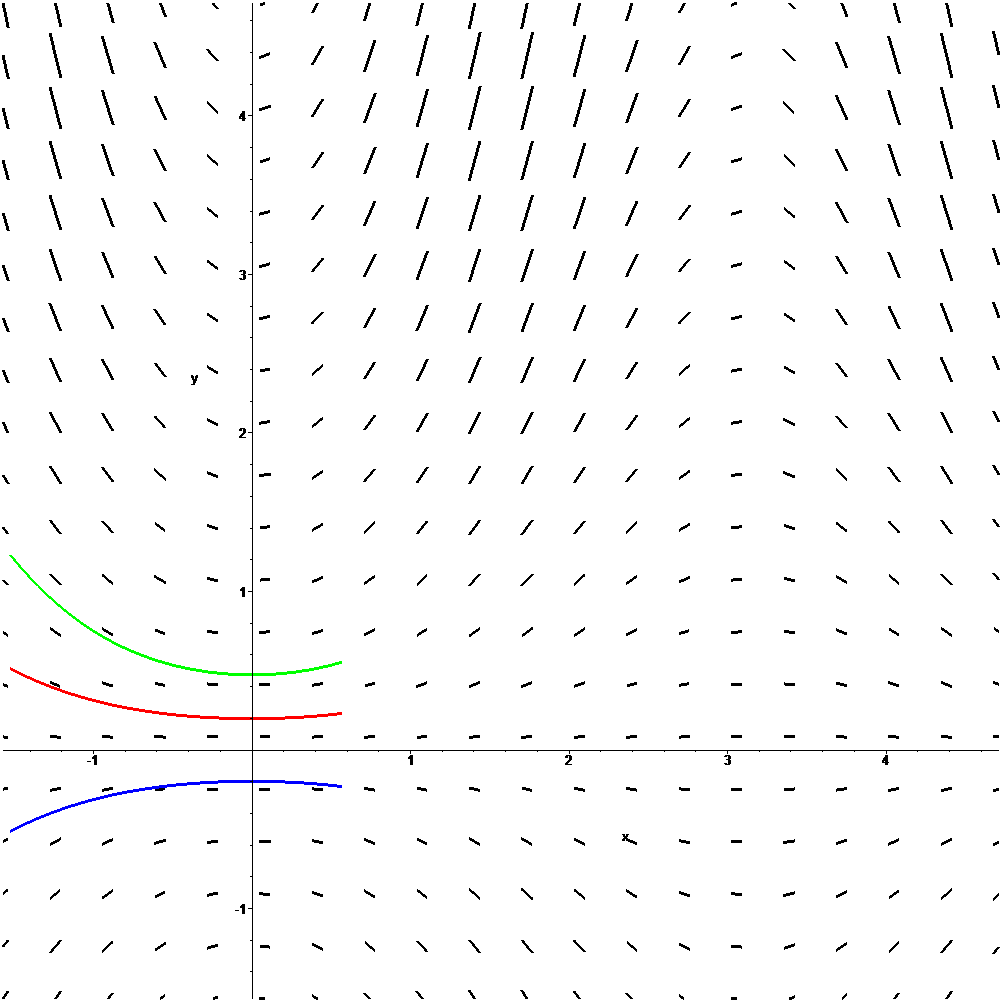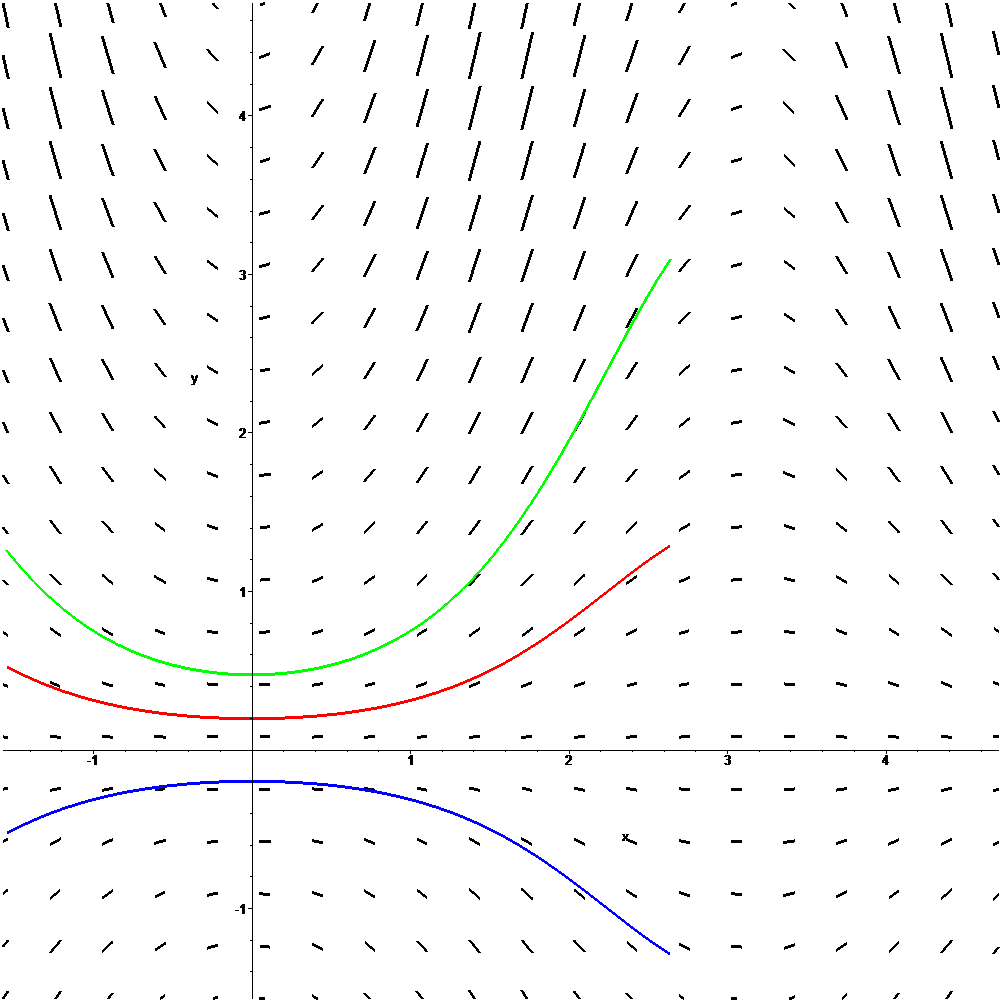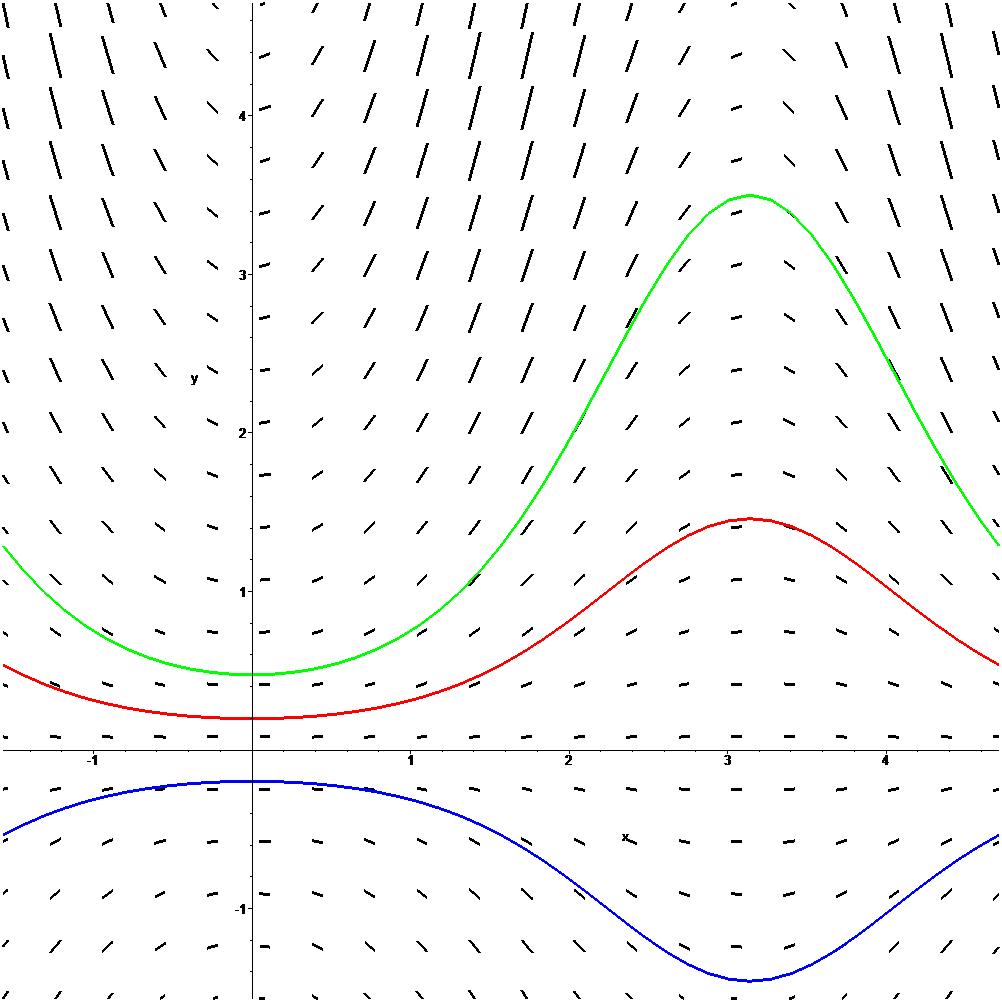
Transparencia añadida
Campo de direcciones de la ecuación diferencial $\quad \textstyle{x'=\cos(tx^2)+\mathrm{sen}\, x,} \quad$ y cuatro de sus trayectorias (o curvas solución).
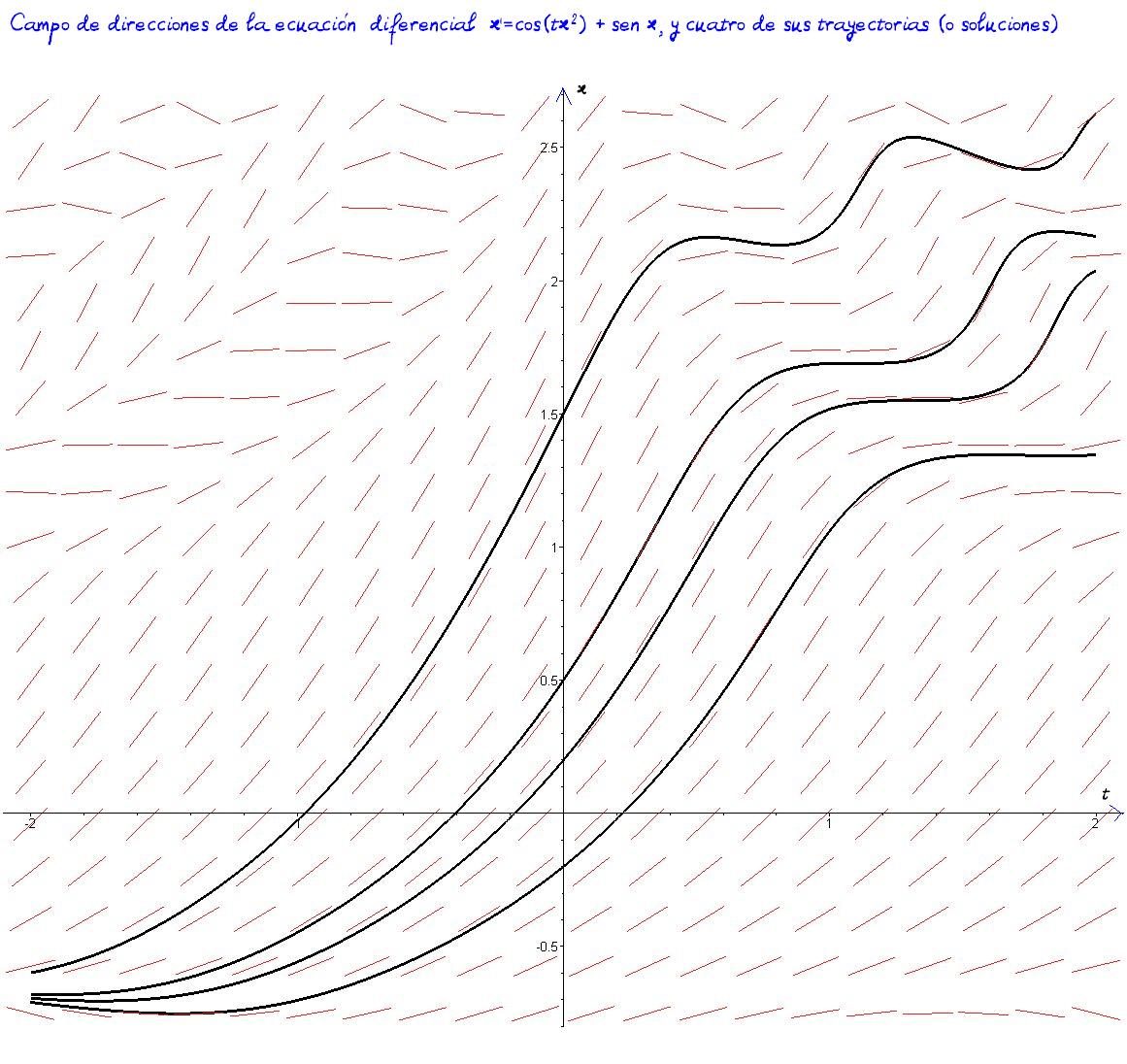
Transparencia 62
$\textstyle{x'=2x-t}$
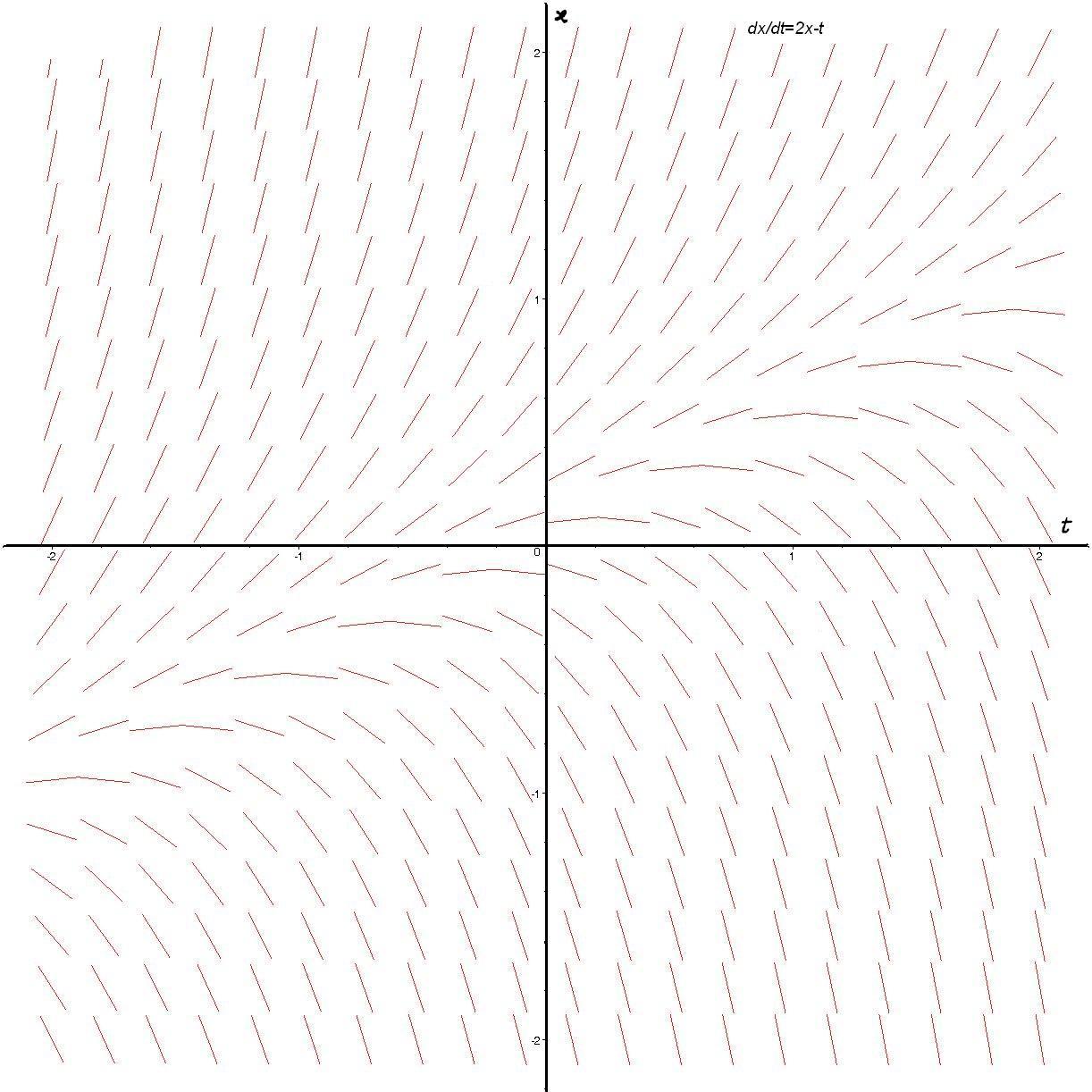
Transparencia 63
$\textstyle{x'=2x-t}$
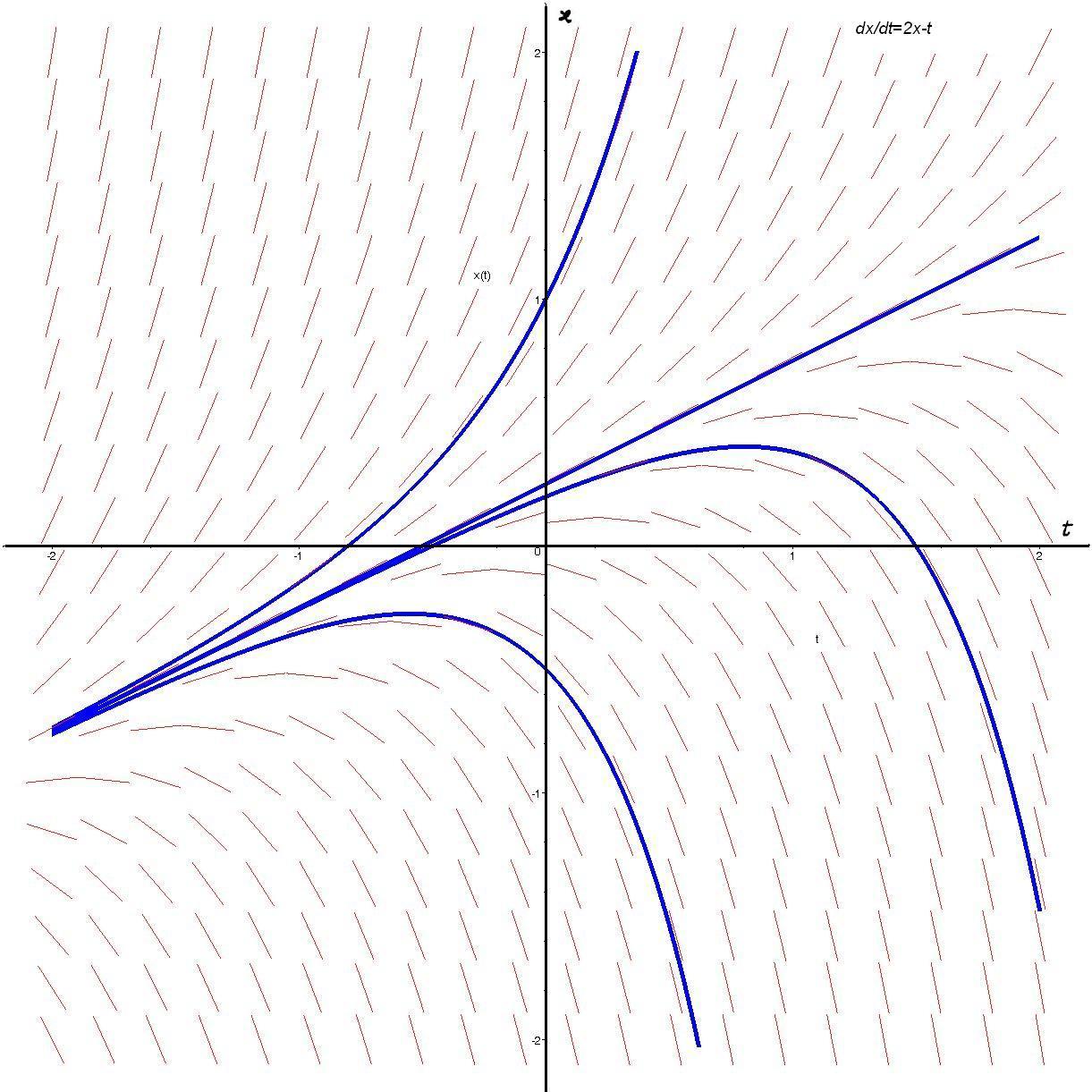
Trayectorias de la ecuación diferencial $\textstyle{x'=2x-t}$ en el cuadrado $\textstyle{-2< t < 2, -2 < x < 2.}$

Transparencia 64:
La ecuación diferencial $\textstyle{x'=3x(1-x)}$ es autónoma.
.jpg)
Transparencia 65
$\textstyle{x'=3x(1-x)}$
_8.jpg)
Trayectorias de la ecuación diferencial autónoma $\textstyle{x'=3x(1-x)}$ en el cuadrado $\textstyle{-2< t < 2, -2 < x < 2}$.

Transparencia 66
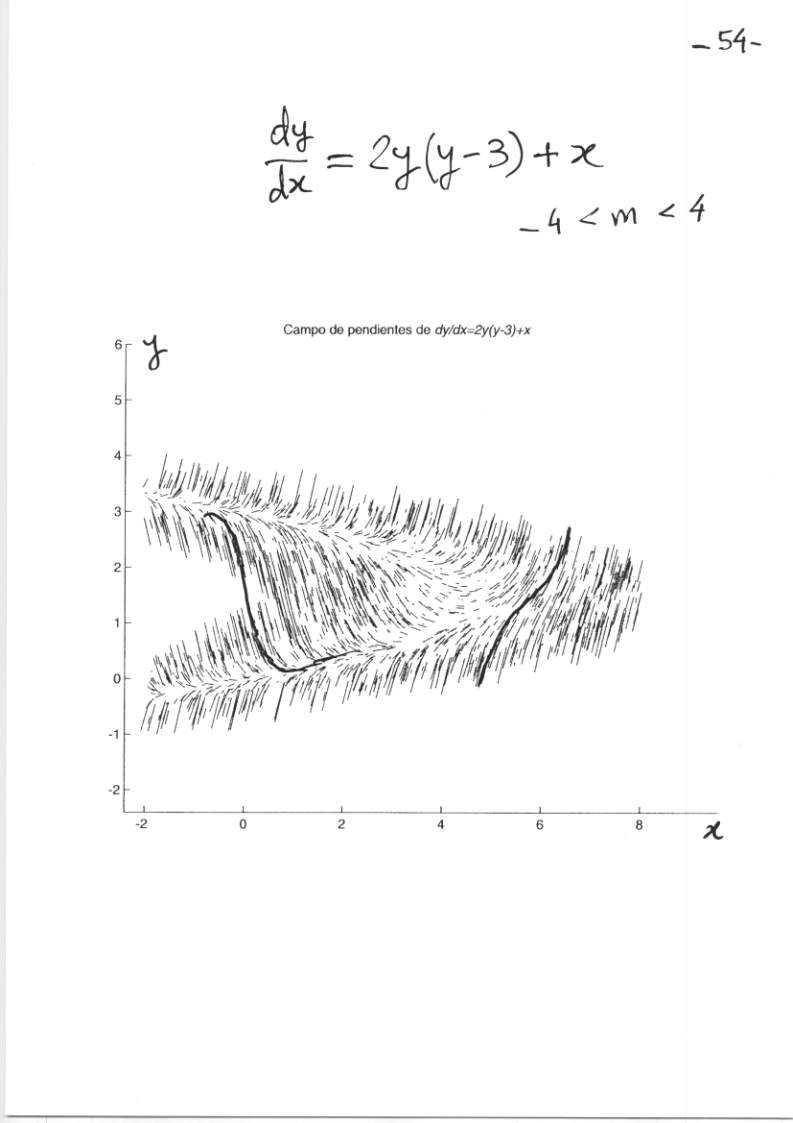
Transparencia 67 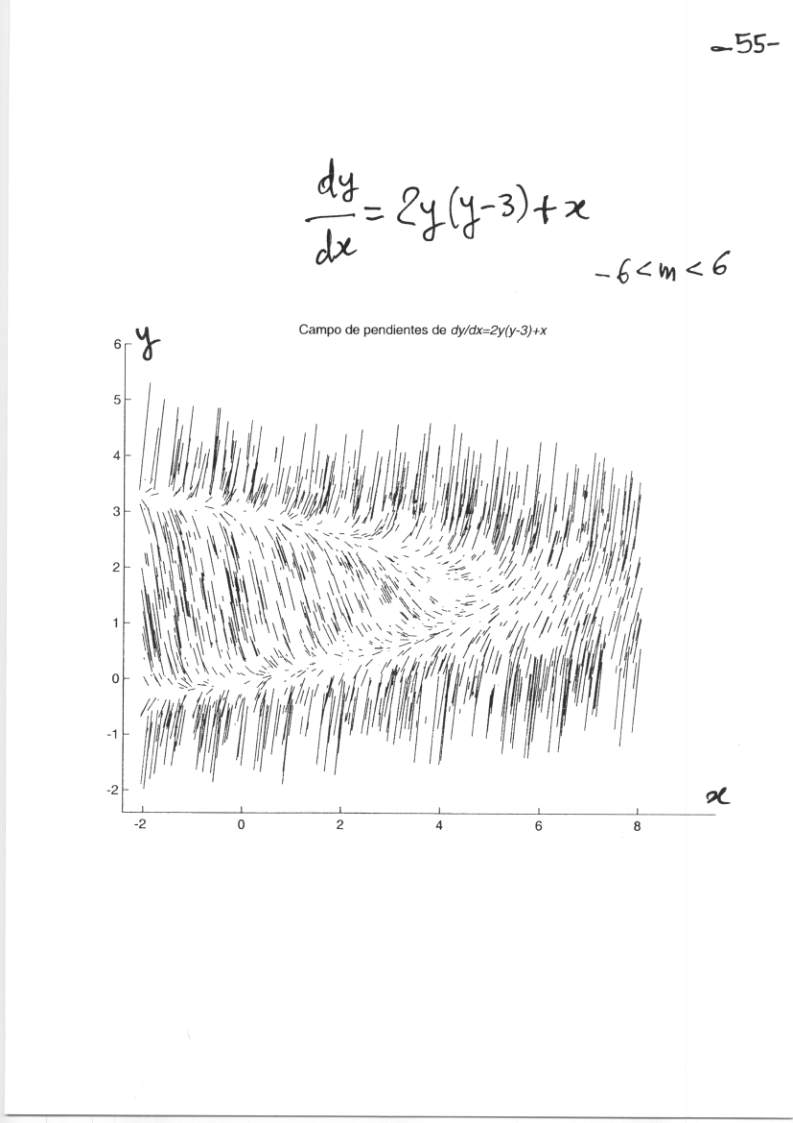
Transparencia 68: MUY IMPORTANTE. 
Transparencia 69
$\textstyle{y'=2y^2-5y+x}$
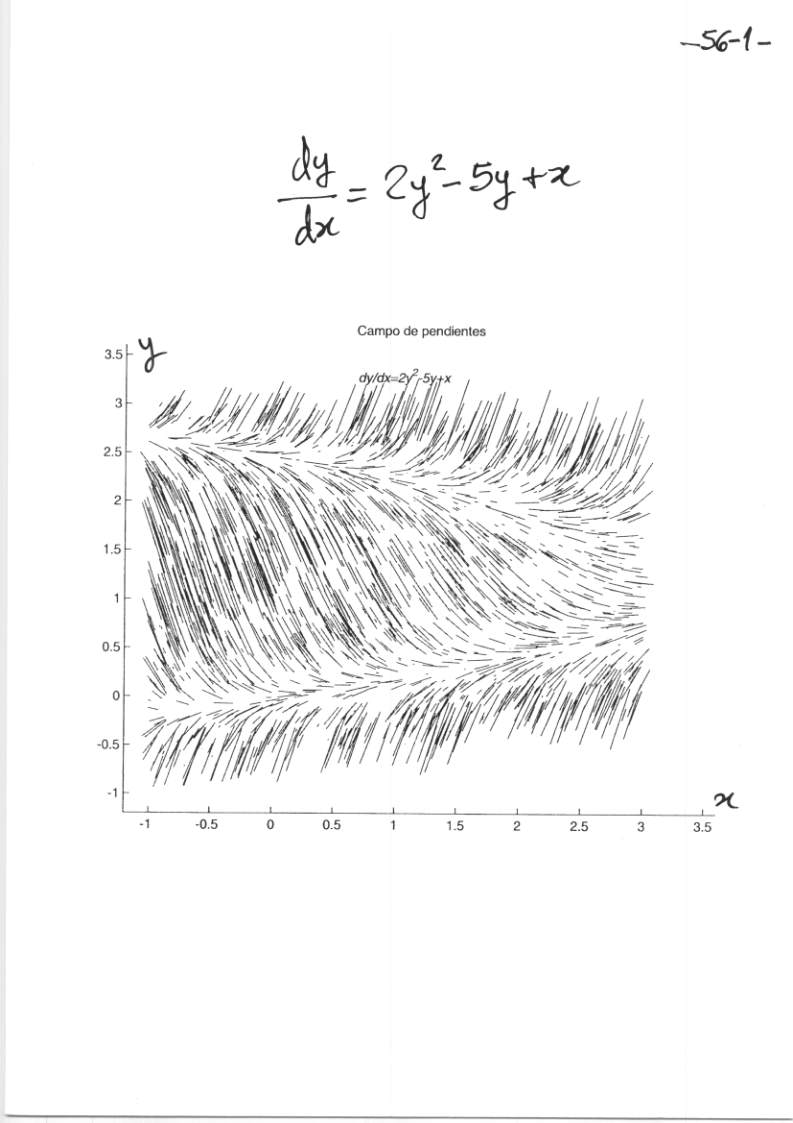
$\textstyle{y'=2y^2-5y+x}$
Aquí enlaza a una película .mpg

La misma película .mpg en blanco y negro.

Transparencia 70
$\textstyle{y'=2y^2-5y+1}$
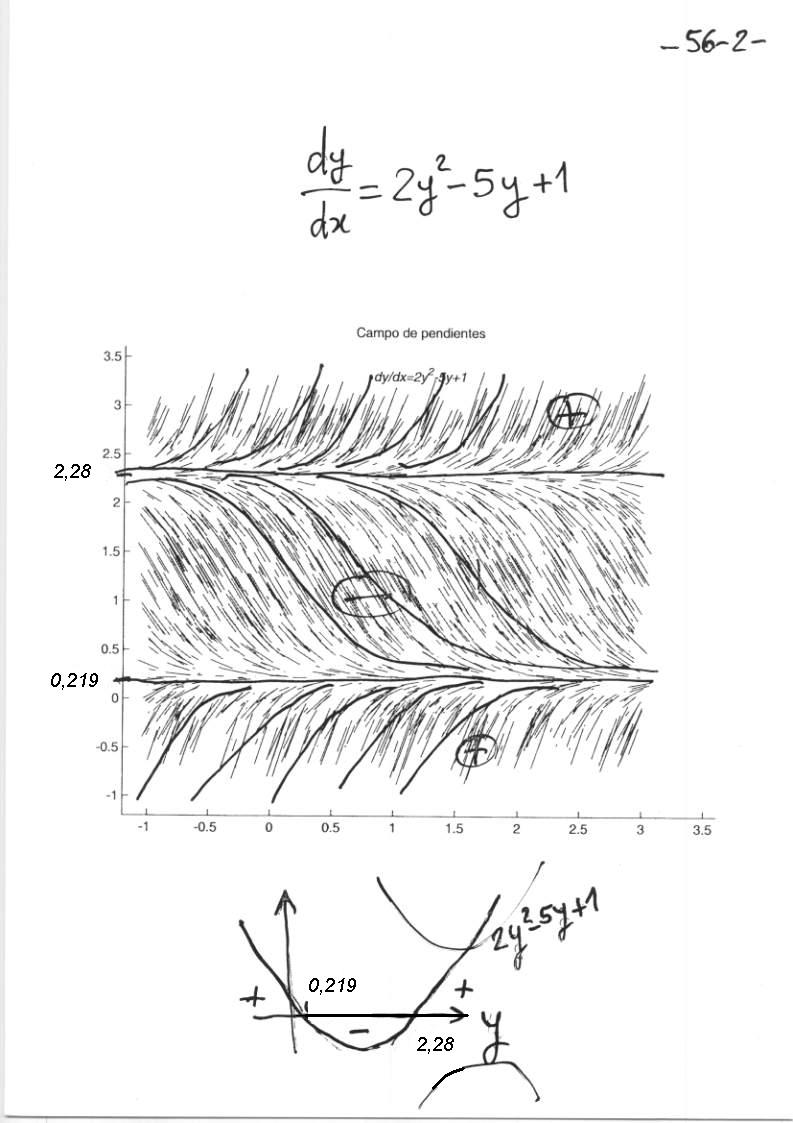
$\textstyle{y'=2y^2-5y+1}$
Película .mpg en blanco y negro: Óbservese que es una
ecuación diferencial autónoma.

