Ecuaciones diferenciales y campos vectoriales

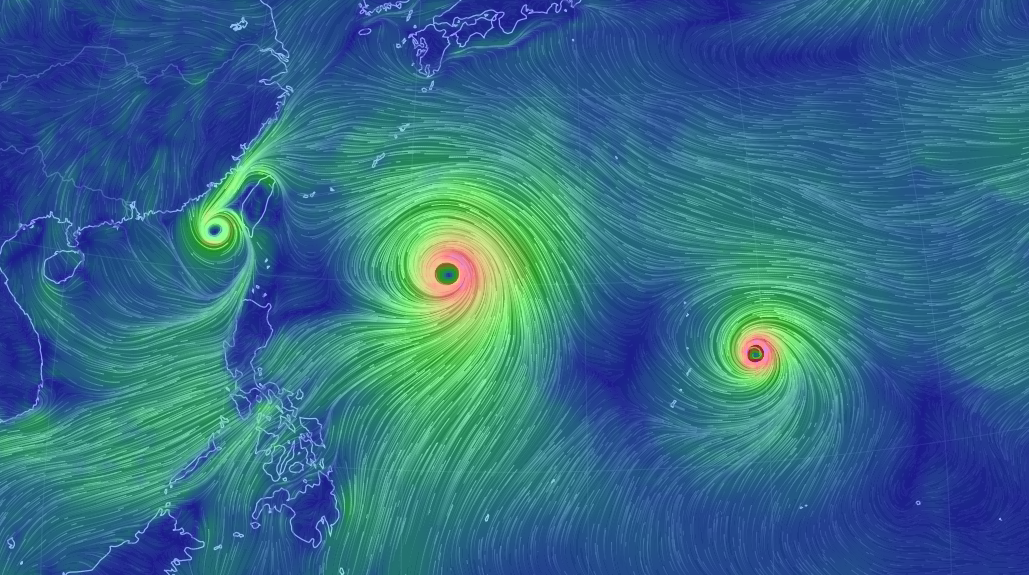
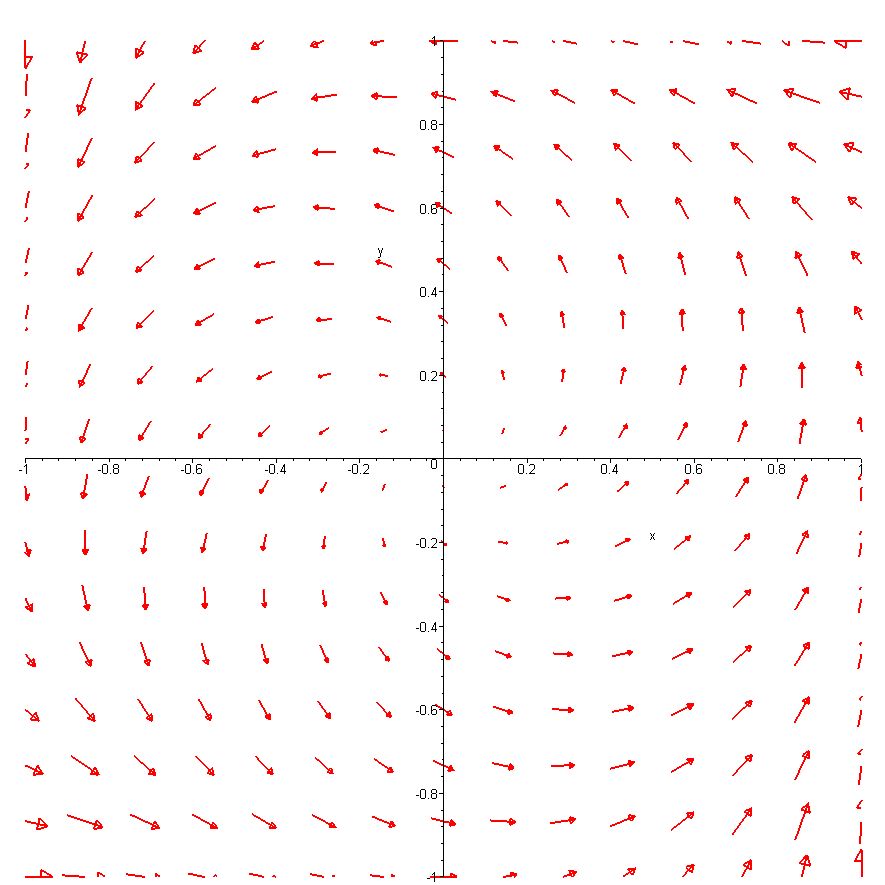
Campo de direcciones o de pendientes de una ecuación diferencial. Campo de un sistema de ecuaciones diferenciales

Trayectorias tangentes a un campo de direcciones

Transparencia 1

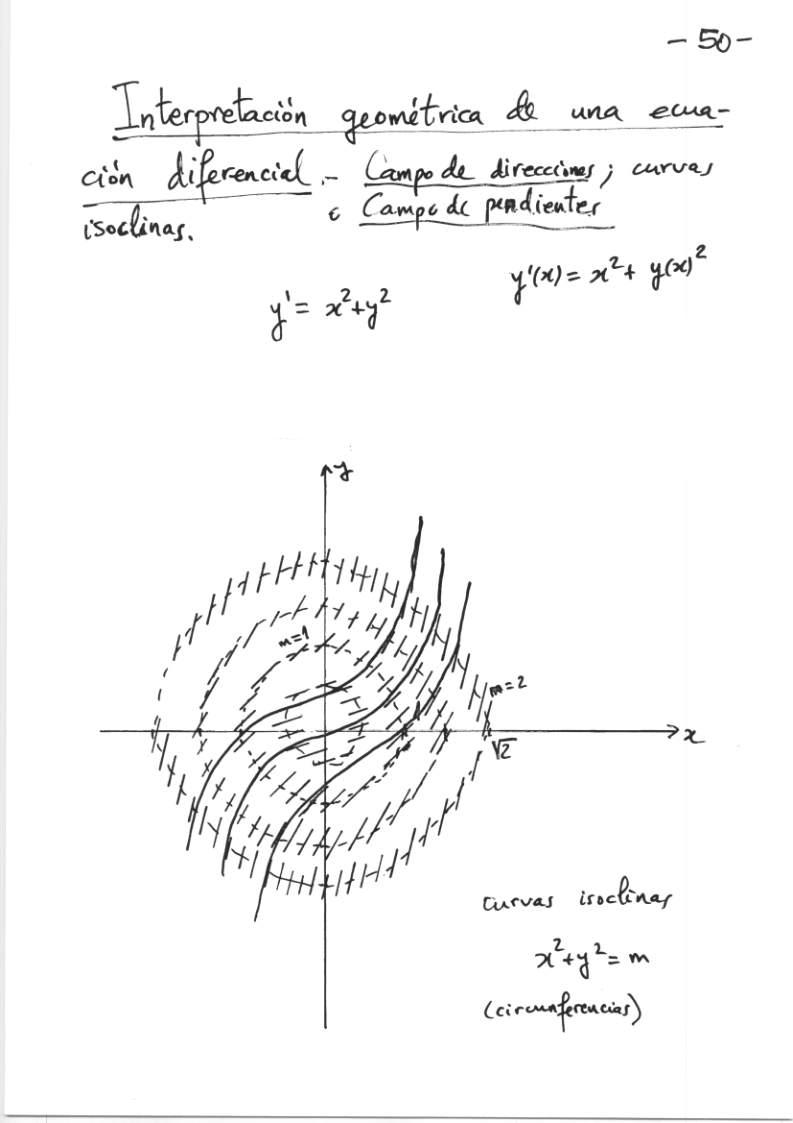
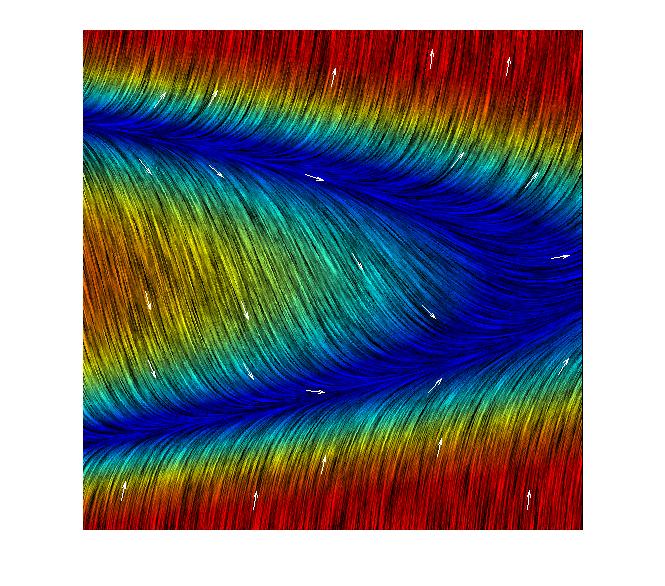
Trayectorias de un sistema de Volterra-Lotka

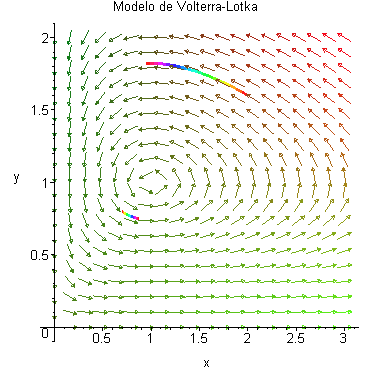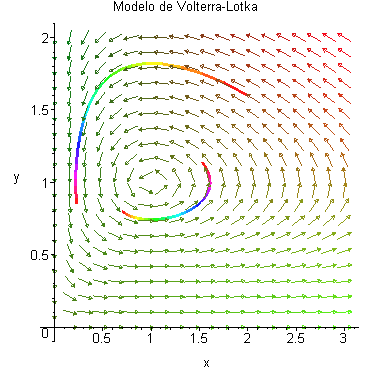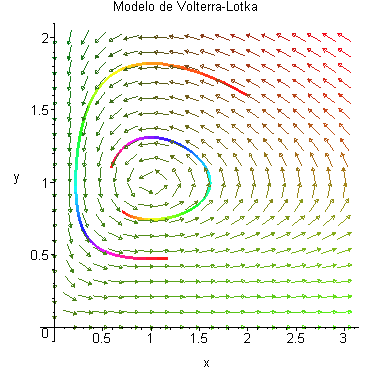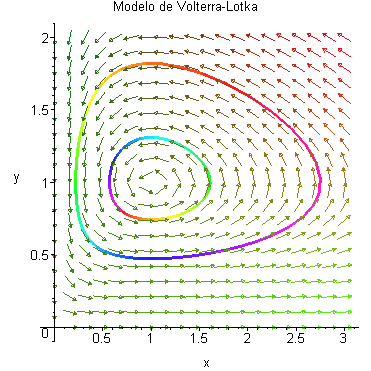
Trayectorias de otro sistema de Volterra-Lotka

Trayectorias tangentes a un campo vectorial.

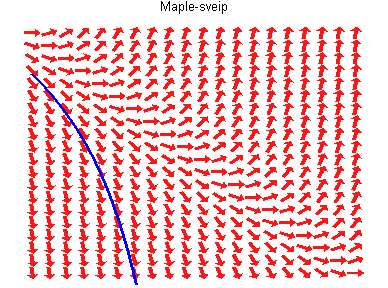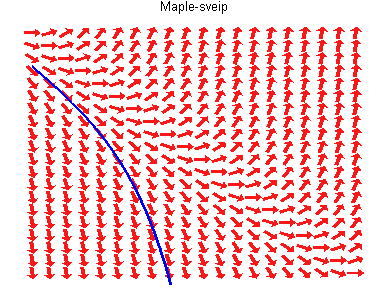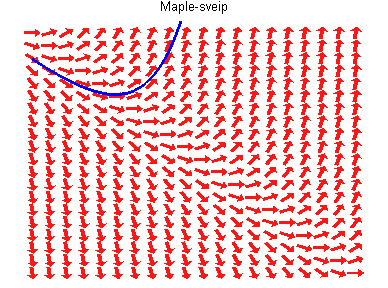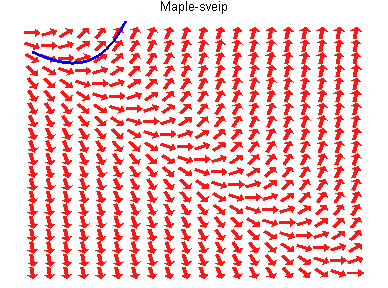
Trayectorias tangentes a un campo vectorial.

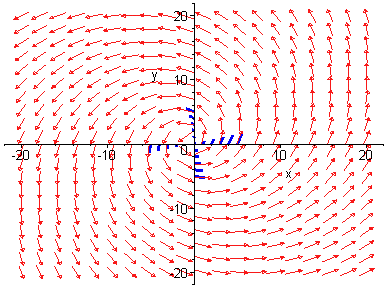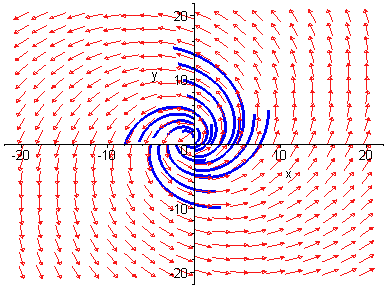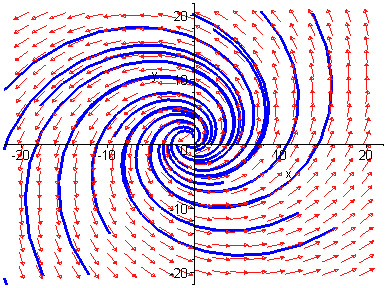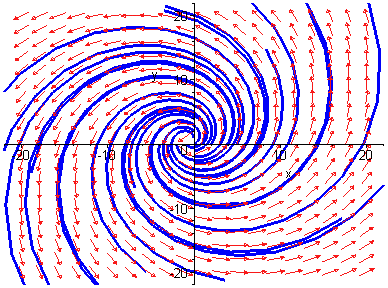
Trayectorias de una ecuación de la forma x'=f(t).

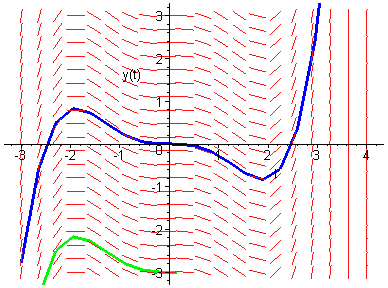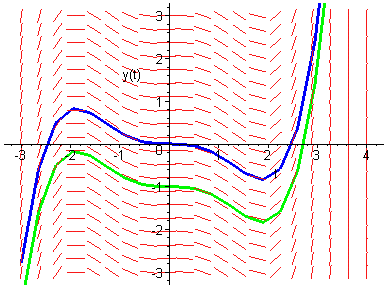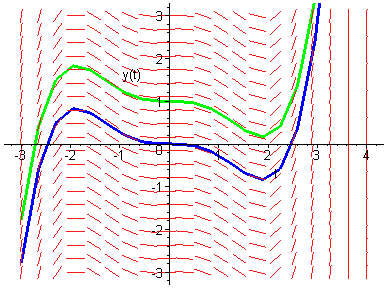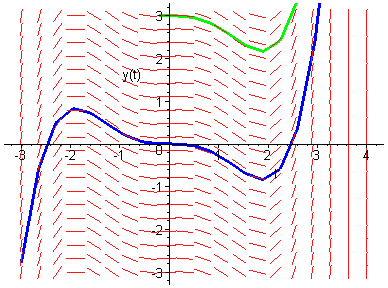
Trayectorias de una ecuación autónoma: x'=f(x).

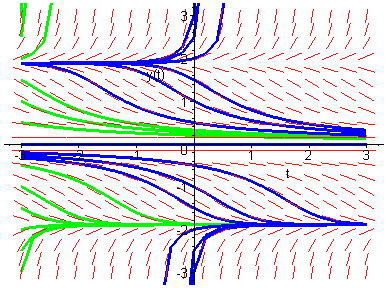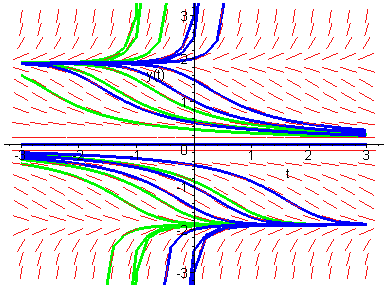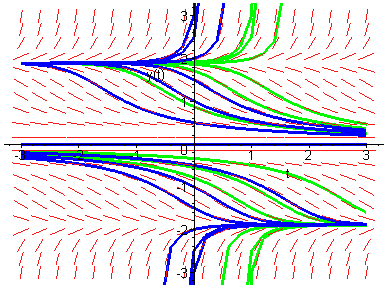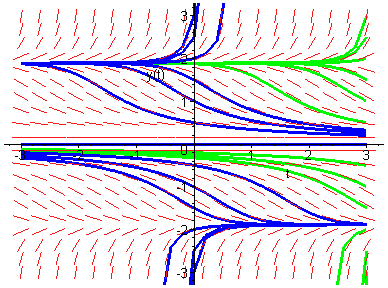
Trayectorias de una familia de ecuaciones diferenciales x'=f(t,x,λ).






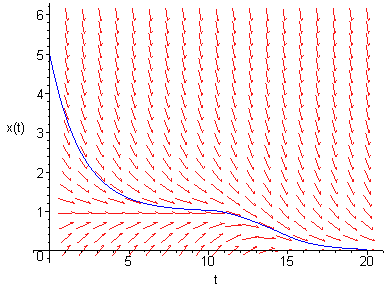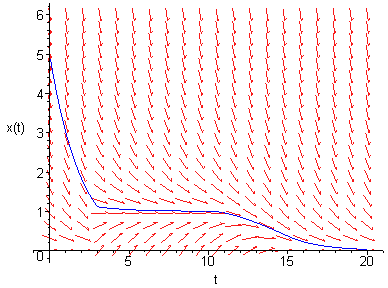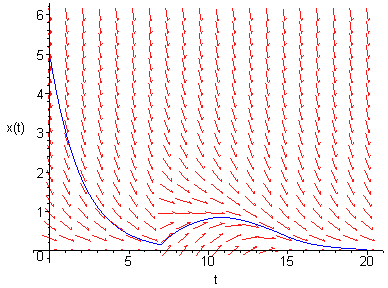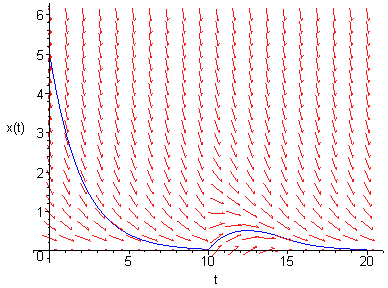
Película sobre la línea de fases de una ecuación diferencial autónoma.

Transparencia 2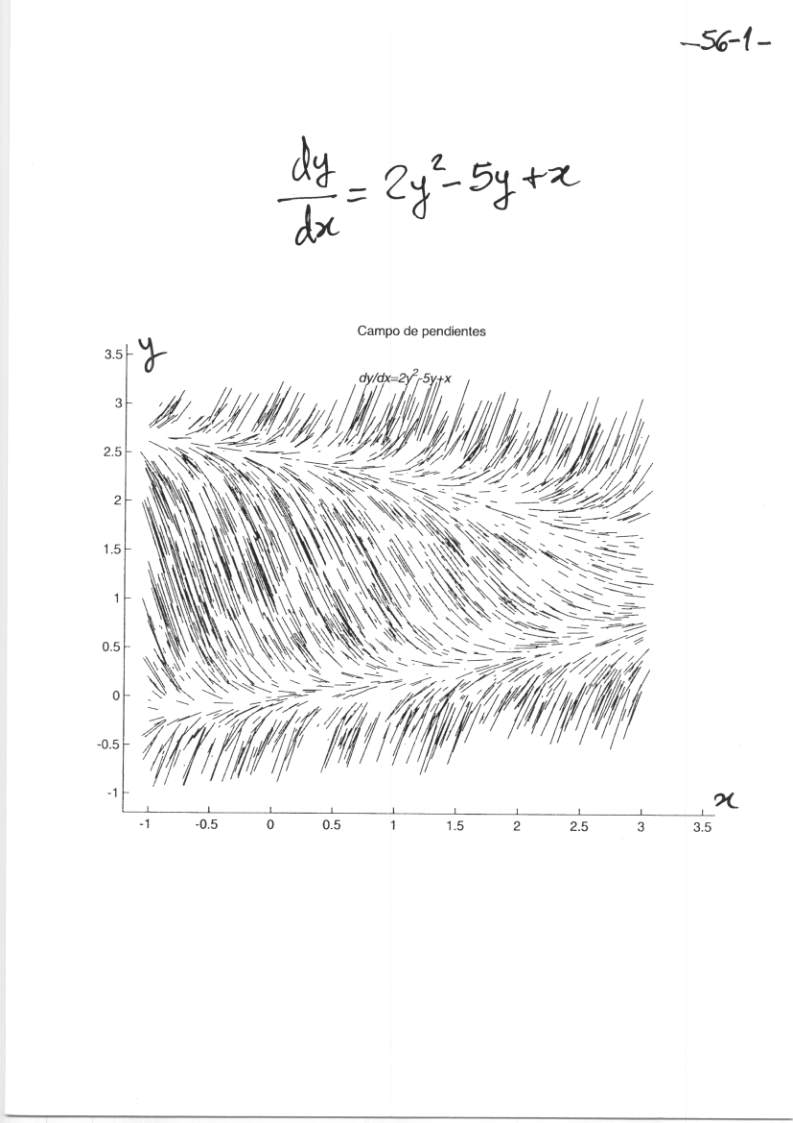

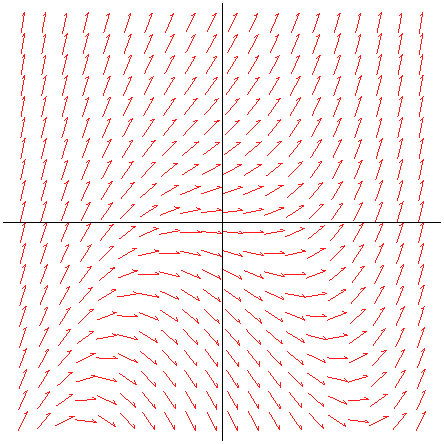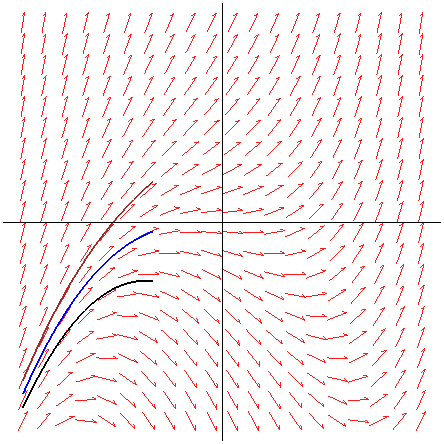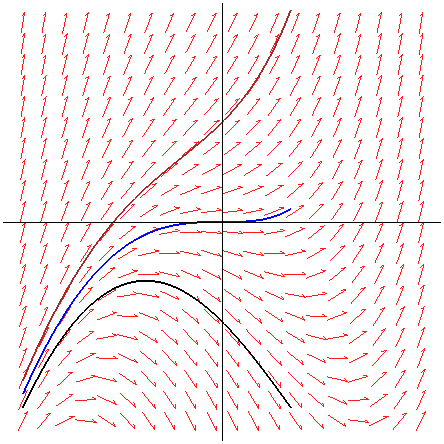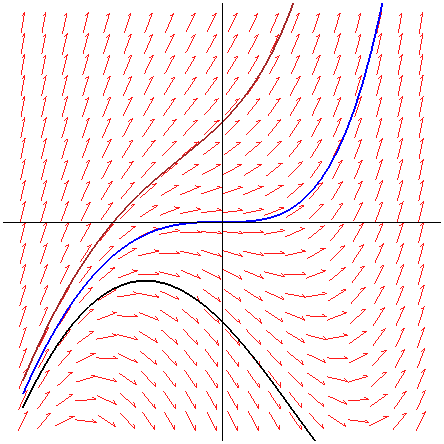
La figura siguiente enlaza a una imagen .gif con trayectorias de la ecuación diferencial

$\displaystyle{ \frac{dy}{dx}=2y^2-5y+x }$

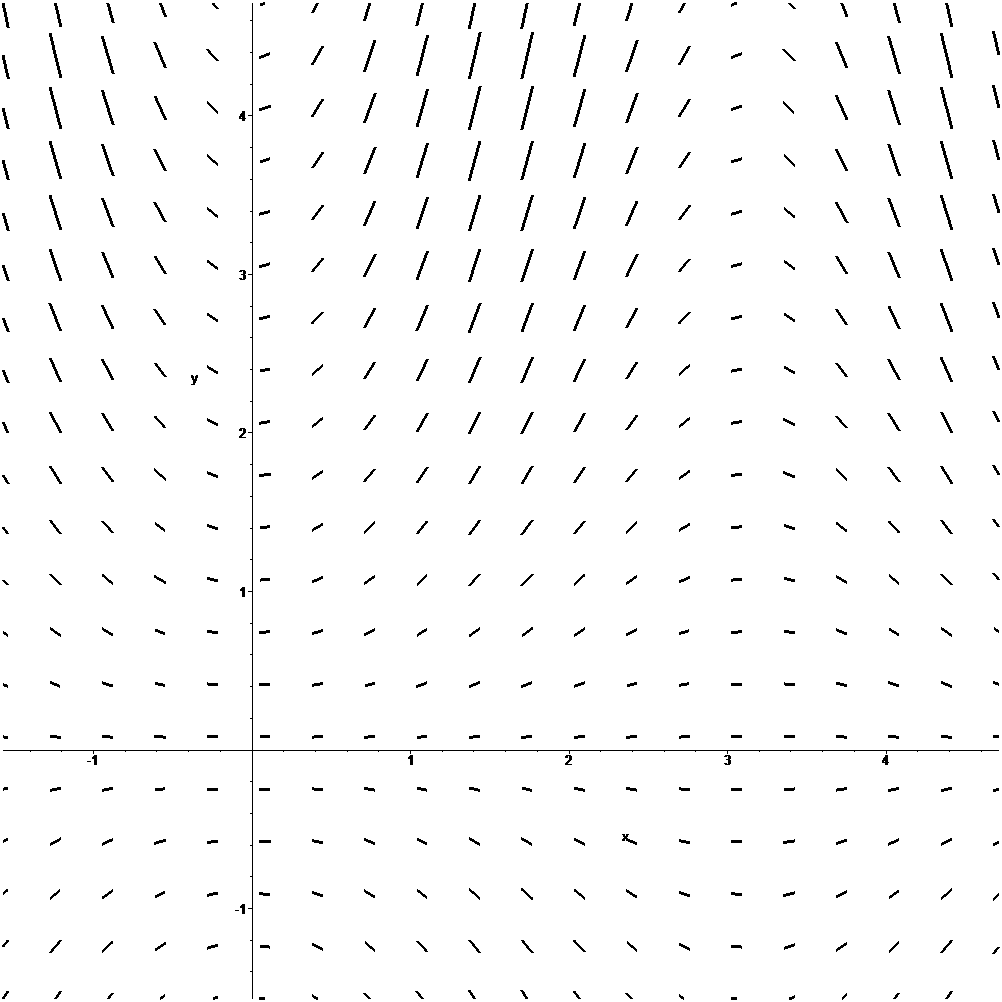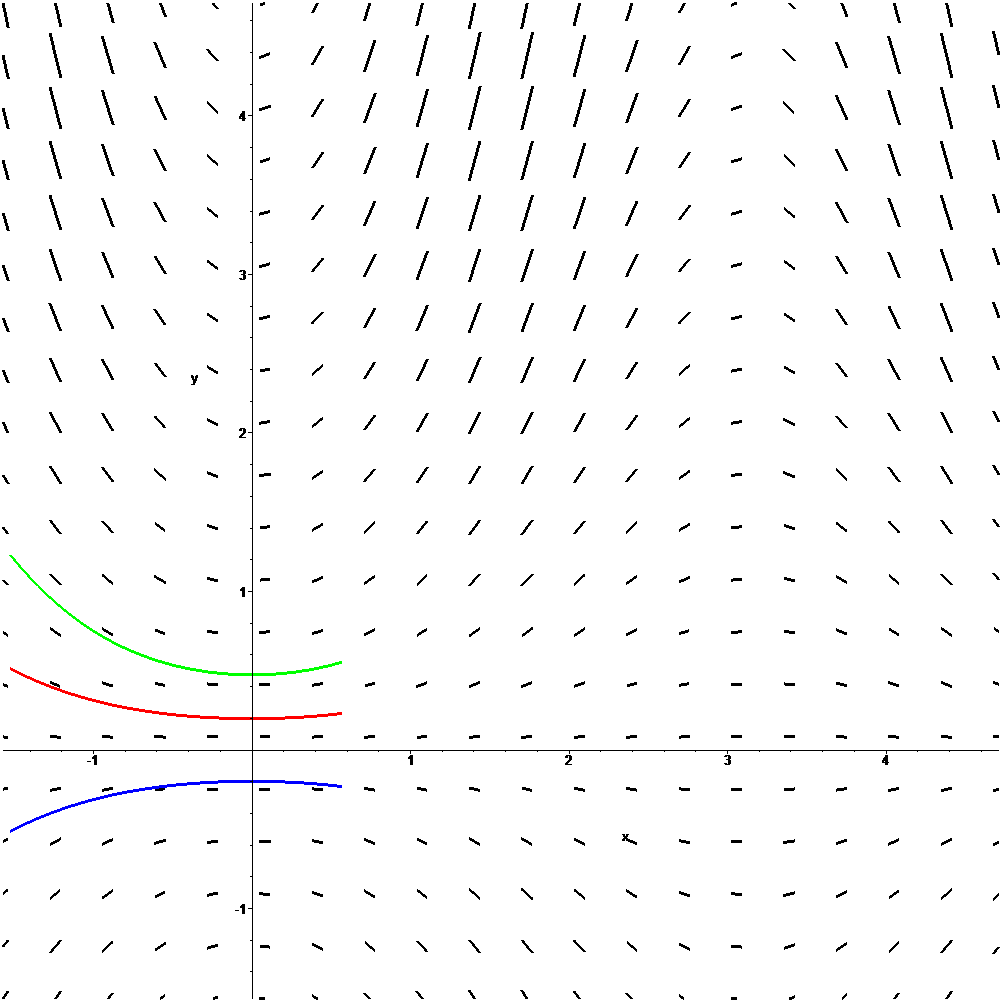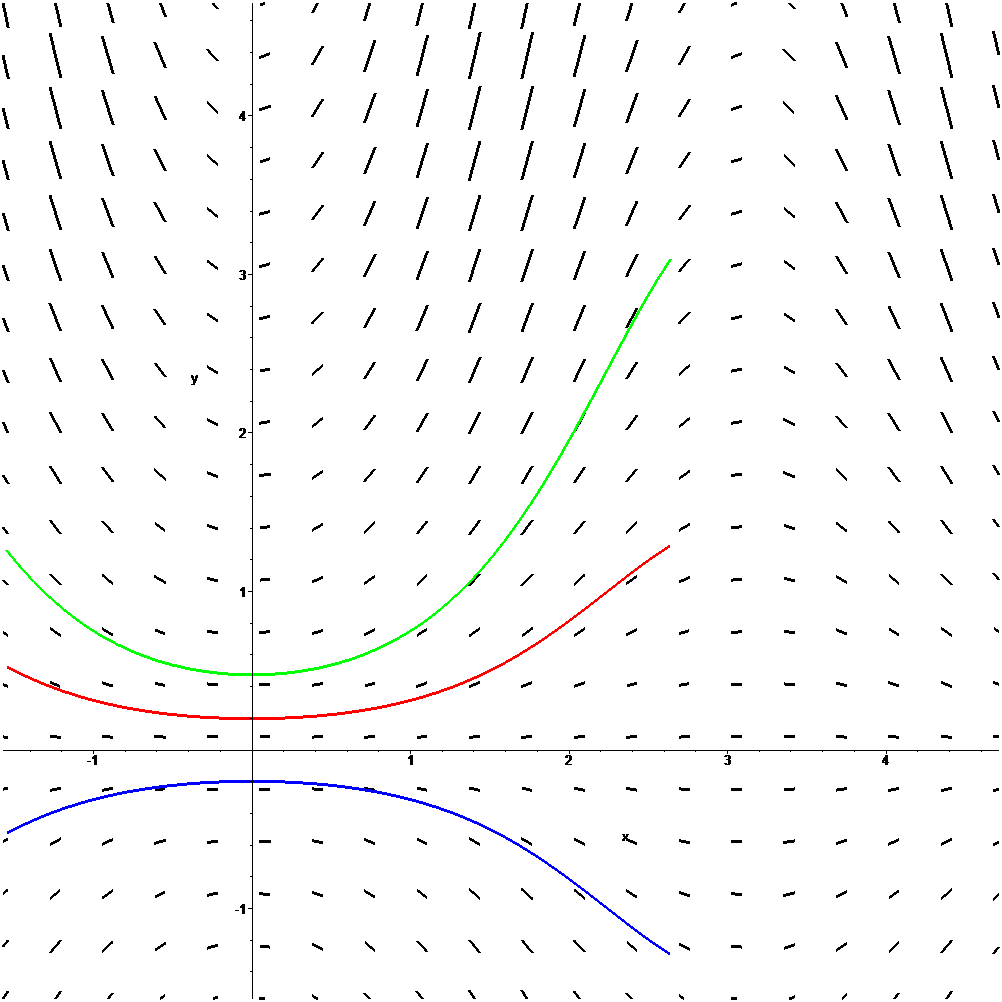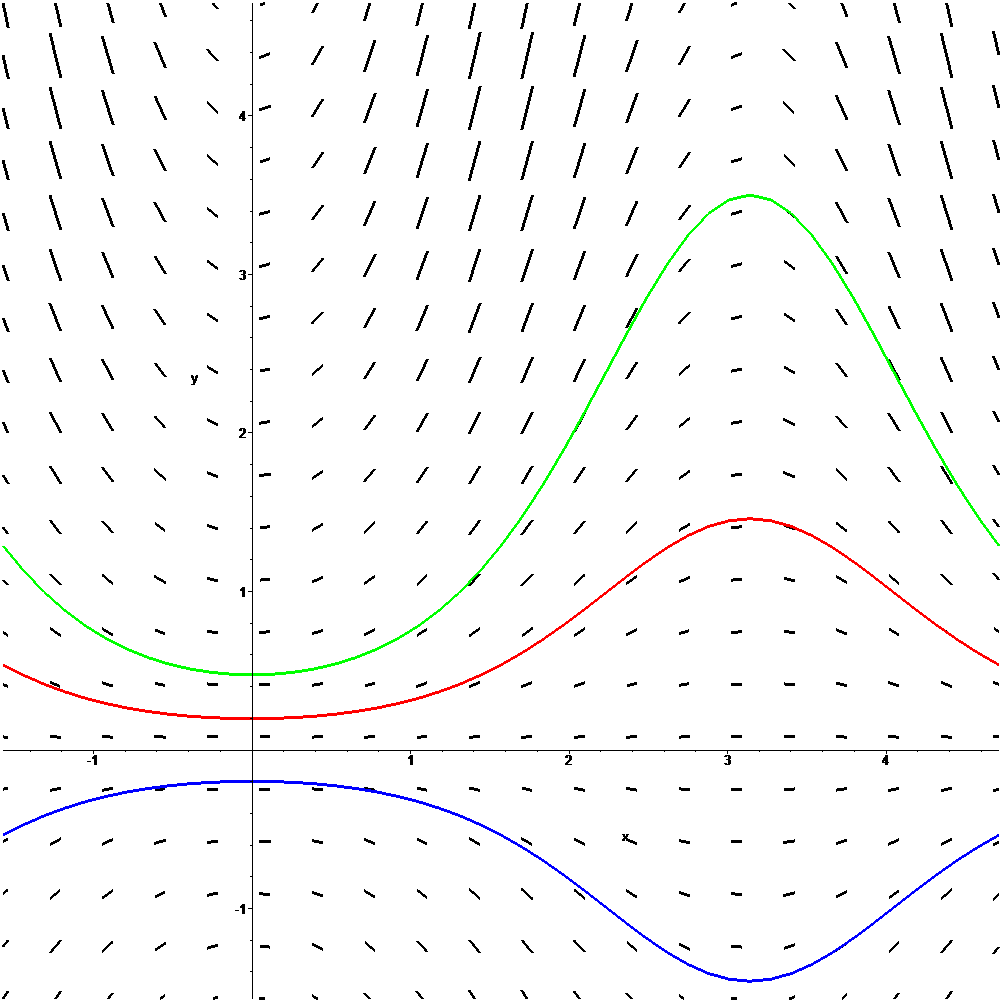
La misma imagen en formato gif en blanco y negro con trayectorias de la ecuación diferencial

$\displaystyle{ \frac{dy}{dx}=2y^2-5y+x }$

Transparencia 3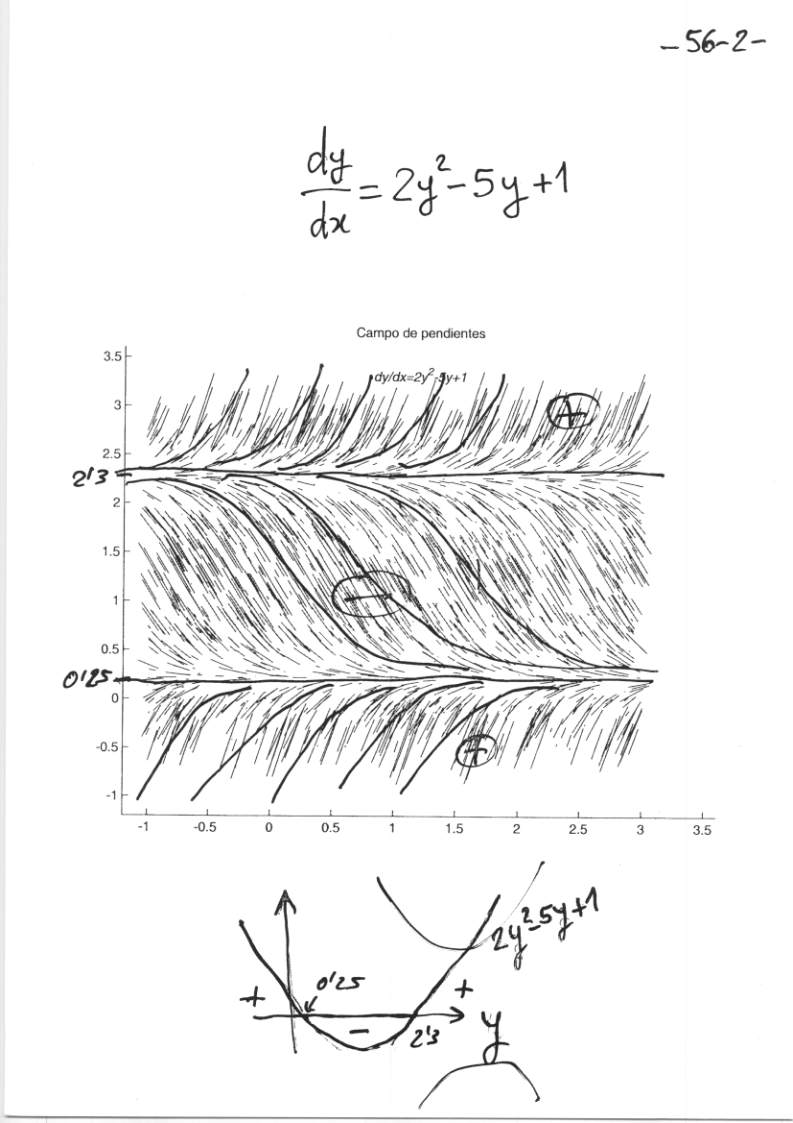

Película .mpg en blanco y negro de la Transparencia 3: Obsérvese que es una ecuación diferencial autónoma.

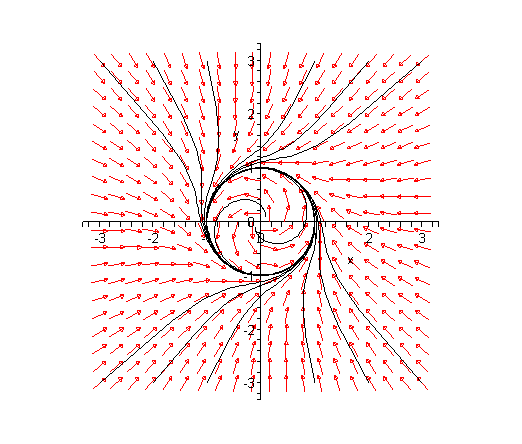
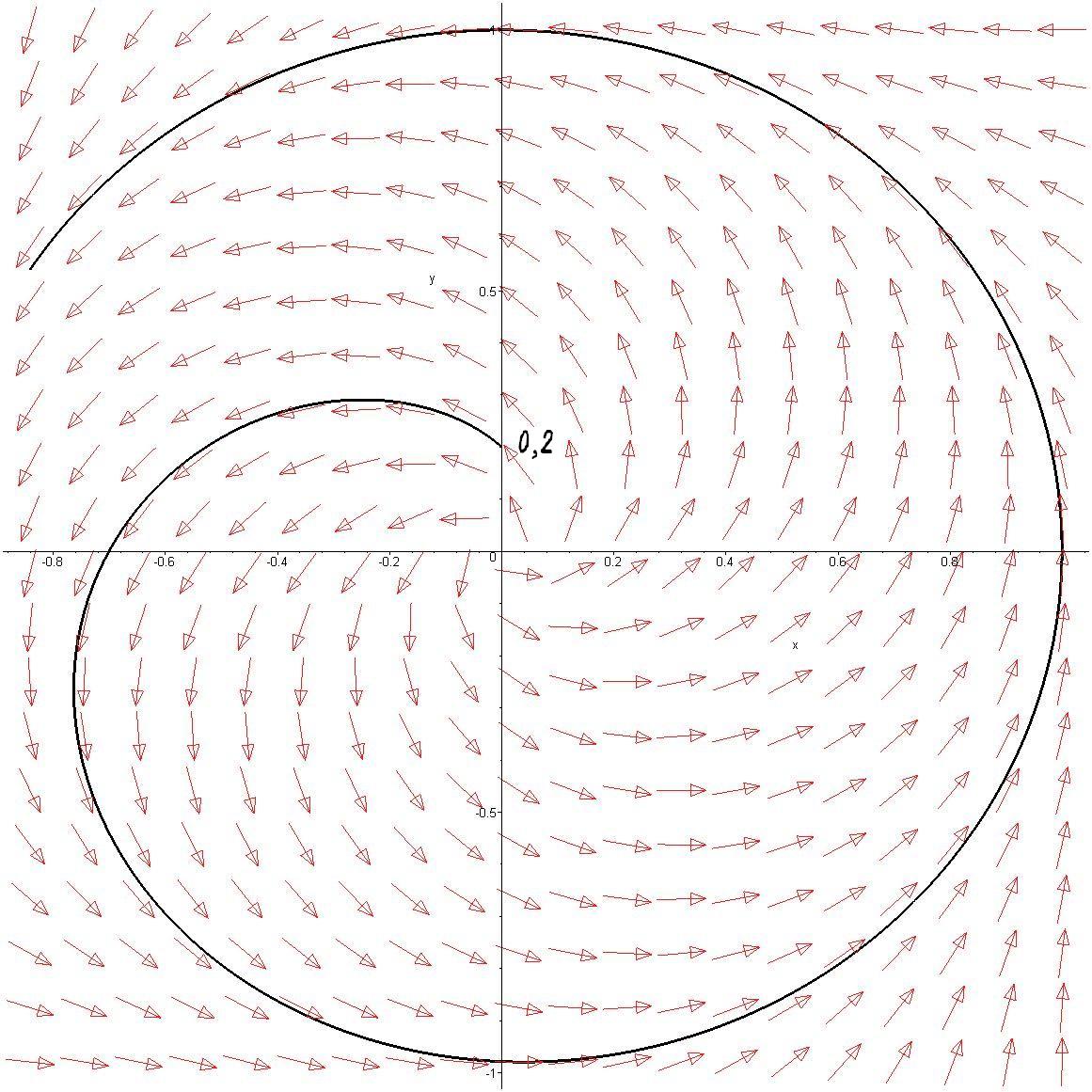
Trayectorias (x(t),y(t)) del sistema diferencial autónomo plano

x'= -y + x(1 - x² - y²),
y'= x + y(1 - x² - y²).

Todas las trayectorias tienden a la circunferencia unidad x² + y²=1 , que es un ciclo límite.

Esto puede verse en las imágenes siguientes.