Carácter: Troncal.
Duración: 1er cuatrimestre.
Créditos: Teóricos: 3, Prácticos: 1,5, Totales: 4,5.
Profesor responsable:
Juan-Miguel Gracia (Grupo 16).
Objetivos generales:
Cálculo diferencial de funciones de
varias variables reales. Se
pondrá énfasis en el significado de las gráficas de funciones
y de las curvas de nivel. Integrales curvilíneas. Nociones de análisis
vectorial.
Programa
Capítulo 1.- Funciones de varias variables reales.
- Curvas de nivel.
- Límites. Continuidad.
- Derivadas parciales y direccionales.
- Diferencial. Gradiente. Puntos críticos.
- Derivadas parciales segundas.
- Condición suficiente de diferenciabilidad.
- Regla de la cadena.
- Aplicaciones geométricas. Conjuntos de nivel. Planos tangentes.
- Matrices jacobianas.
- Máximos, mínimos y puntos de ensilladura.
- Funciones implícitas.
Capítulo 2.- Integral curvilínea.
- Caminos e integrales curvilíneas.
- Otras notaciones para las integrales curvilíneas.
- Propiedades fundamentales.
- Integrales curvilíneas respecto de la longitud de arco.
- Centro de gravedad. Momentos de inercia.
- Conjuntos conexos abiertos. Independencia del camino.
- Teoremas fundamentales del cálculo para integrales curvilíneas.
- Condiciones para que un campo vectorial sea un gradiente.
- Funciones de potencial.
- Diferenciales exactas en dos variables. Factores integrantes.
Capítulo 3.- Análisis vectorial.
- Campos escalares y vectoriales.
- El gradiente de un campo escalar.
- El rotacional y la divergencia de un campo vectorial.
- Un campo vectorial es un gradiente si y sólo si su rotacional es cero.
- Otras propiedades del rotacional y la divergencia.
- Reconstrucción de un campo vectorial a partir de su rotacional.
- Diferenciales exactas en tres variables. Existencia de factores integrantes.
Bibliografía
Teoría y enunciados de problemas
- T.M. Apostol: Calculus, 2 volúmenes, Reverté, Barcelona, 1978.
Claro; riguroso. El volumen 2 se usará para toda la asignatura.
- Marsden y Tromba: Cálculo Vectorial. Didáctico con muy buenas figuras.
- R. Courant y F. John: Introducción al Cálculo y al Análisis Matemático ,
Novena reimpresión, Limusa, México, 1999. Un libro clásico, que une la imaginación intuitiva y el razonamiento
deductivo.
Problemas resueltos
- M.R. Spiegel: Teoría y problemas de cálculo avanzado, Colección Schaum, McGraw-Hill.
- Demidovich: 5000 problemas de análisis matemático.
- Bombal, Rodríguez Marín, Vera: Problemas de análisis matemático,
tomo 2. Cálculo diferencial, Editorial AC, Madrid, ¡nivel alto!
Conocimientos previos
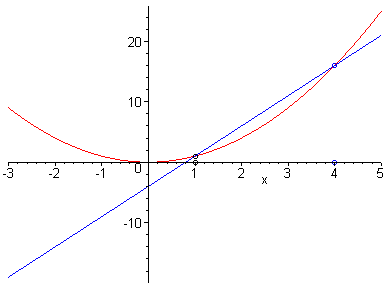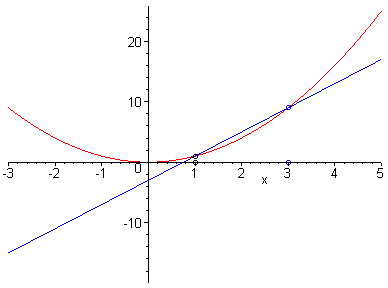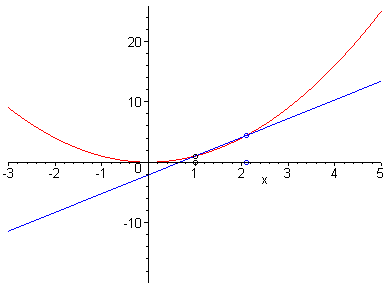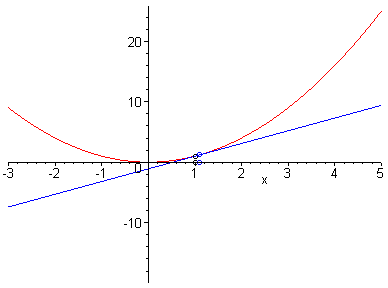
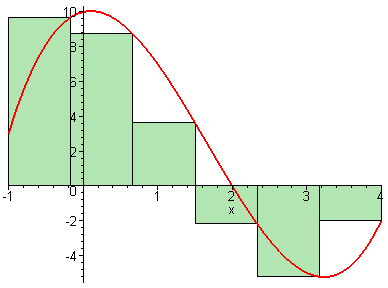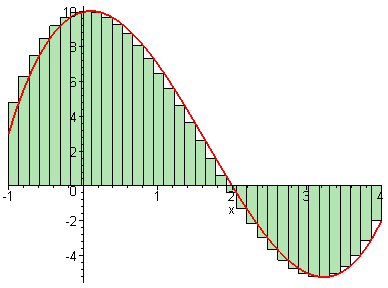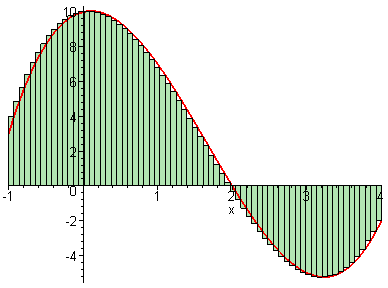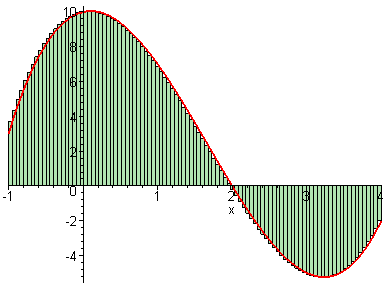
Sería muy conveniente que el estudiante que vaya a cursar esta
asignatura, entienda los conceptos sugeridos por las dos imágenes
animadas siguientes y la relación entre ambas.
Portada
de la Sección Departamental
Modificada el 25 de febrero de 2005.
Páginas administradas por Juan-Miguel Gracia:




