Carácter: troncal.

Duración: 1^er cuatrimestre.

Créditos: teóricos: 3, prácticos: 1,5, totales: 4,5.

Juan-Miguel Gracia (Grupo 16).

Cálculo diferencial de funciones de varias variables reales. Se pondrá énfasis en el significado geométrico de las gráficas de funciones y los mapas de las curvas y superficies de nivel.

1. Curvas de nivel.
2. Límites. Continuidad.
3. Derivadas parciales y direccionales.
4. Diferencial. Gradiente. Puntos críticos.
5. Derivadas parciales segundas.
6. Condición suficiente de diferenciabilidad.
7. Regla de la cadena.
8. Aplicaciones geométricas. Conjuntos de nivel. Planos tangentes.
9. Máximos, mínimos y puntos de ensilladura.

Capítulo 2.- Espacio euclídeo.

1. Vectores.
2. Producto escalar.
3. Desigualdad de Schwarz. Teorema de Pitágoras.
4. Método de ortogonalización de Gram-Schmidt.
5. Distancia de un vector a un subespacio.
6. Ajuste por mínimos cuadrados.

1. T.M. Apostol: Calculus, 2 volúmenes, Reverté, Barcelona, 1978. Claro; riguroso. El volumen 2 se usará para toda la asignatura.
2. Marsden y Tromba: Cálculo vectorial. Didáctico con muy buenas figuras.
3. R. Courant y F. John: Introducción al cálculo y al análisis matemático , novena reimpresión, Limusa, México, 1999. Un libro clásico, que une la imaginación intuitiva y el razonamiento deductivo.
4. S. Lang: Álgebra lineal, Fondo Educativo Interamericano, 1993. Elemental, recomendado para el Capítulo 2.

1. M.R. Spiegel: Teoría y problemas de cálculo avanzado, Colección Schaum, McGraw-Hill.
2. Demidovich: 5000 problemas de análisis matemático.
3. Bombal, Rodríguez Marín, Vera: Problemas de análisis matemático, tomo 2. Cálculo diferencial, Editorial AC, Madrid, ¡nivel alto!

Conocimientos previos

1. Funciones de una variable real:
   1. idea intuitiva de límite y continuidad;
   2. saber derivar funciones elementales;
   3. derivabilidad: concepto y definición;
   4. interpretación física de la derivada: velocidad;
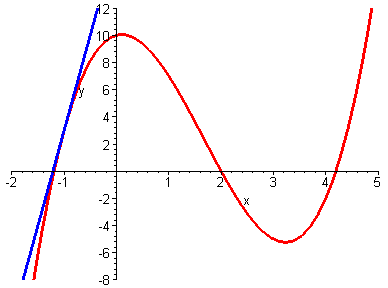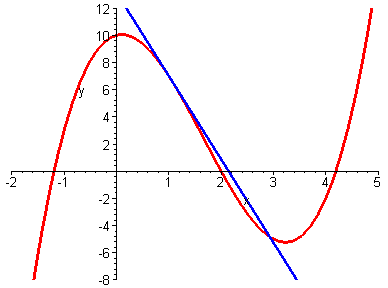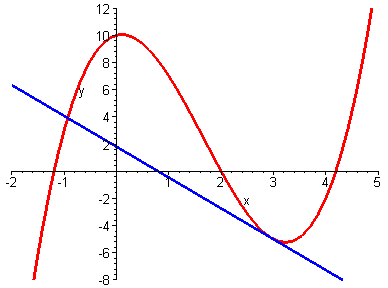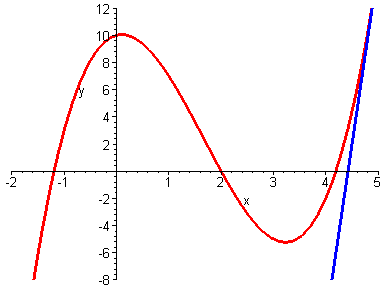
   5. interpretación geométrica de la derivada: recta tangente;
   6. recta tangente y=mx+b a una curva y=f(x); la pendiente m=f'(x); tangente de un ángulo; relaciones entre estos conceptos;
   7. teorema de valor medio;
   8. las funciones con derivada nula son constantes;
   9. intervalos donde una función es monótona: creciente o decreciente;
   10. máximos y mínimos relativos;
   11. intervalos donde una función es cóncava o convexa; puntos de inflexión;
2. Funciones elementales:
   1. Exponencial f(x)=e^x : f'(x)=e^x; Para todo número real x se tiene que e^x > 0; e^x es una función estrictamente creciente; lím _{x → ∞} e^x = ∞ ; lím _{x → -∞} e^x = 0; e^x+y = e^xe^y ; e⁰ = 1. Esta es la función más importante de las Matemáticas.
   2. Logaritmo neperiano ln x : función recíproca o inversa de e^x; ln (xy) = ln x + ln y; ln 1 = 0; lím _{x → 0+} ln x = -∞ ; lím _{x → ∞} ln x = ∞ ;
   3. sen x ; cos x ; tg x ; arcsen x ; arccos x ; arctg x .
3. Geometría:
   1. Medida de un ángulo en radianes.
   2. Tangente de un ángulo.
   3. Producto escalar de vectores. Producto vectorial de vectores de tres dimensiones.
   4. Rectas en el plano. Vector normal a una recta.
   5. Rectas y planos en el espacio. Vector normal a un plano.
   6. Distancia de un punto a un plano.
   7. Ecuación de la circunferencia y de la elipse.
   8. Recta tangente a una circunferencia en un punto.
   9. Ecuación de una esfera.
   10. Plano tangente a una esfera en un punto.

Portada de la sección departamental

Modificada el 27 de septiembre de 2005.

Páginas administradas por Juan-Miguel Gracia: