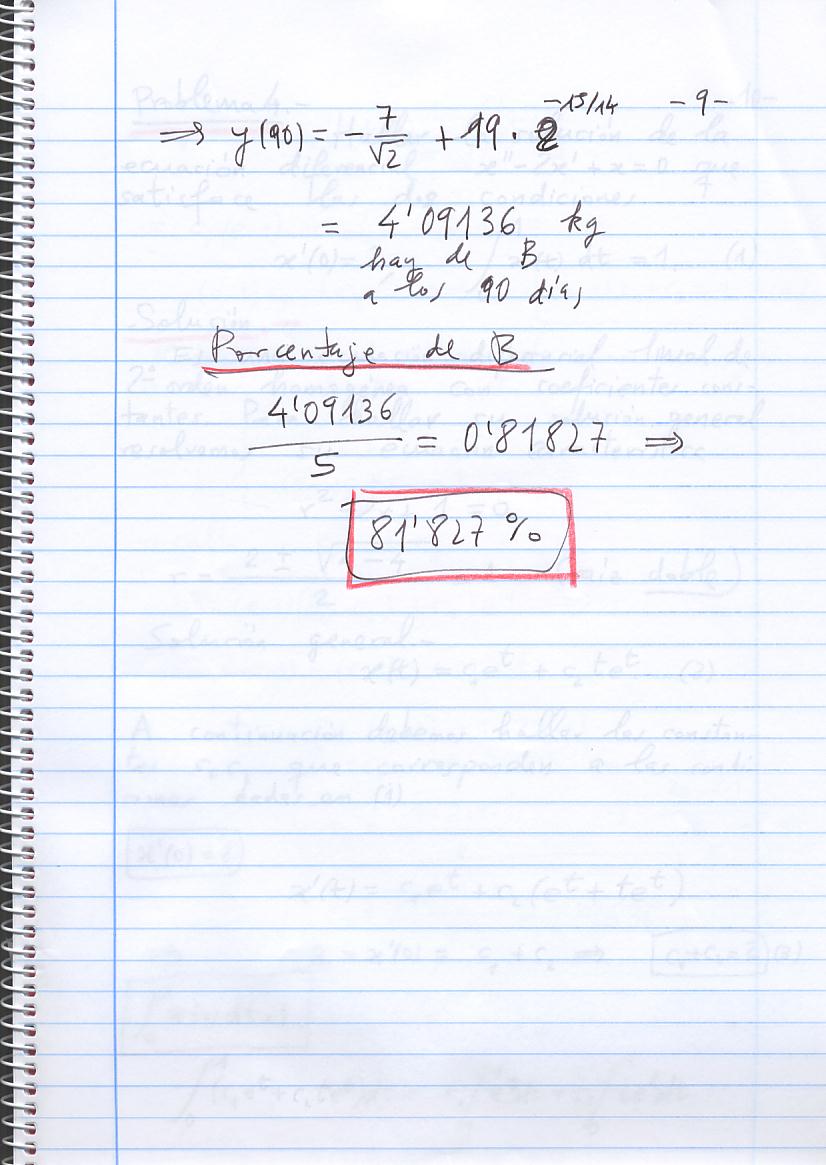Soluciones breves
Problema 1




Problema 2




Problema 3
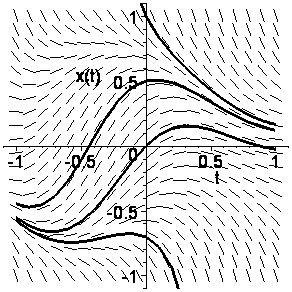
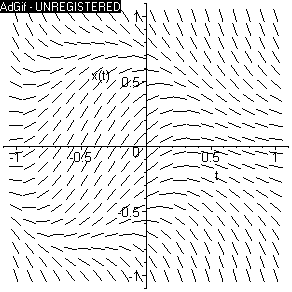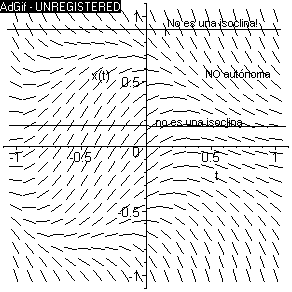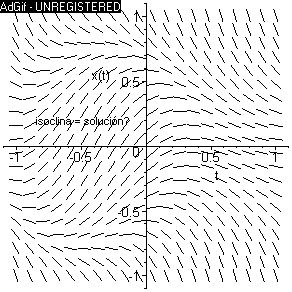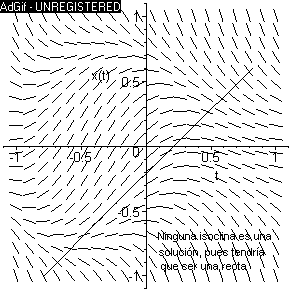
Consideremos una ecuación diferencial de primer orden cuyo campo de
pendientes viene dado en la figura siguiente.
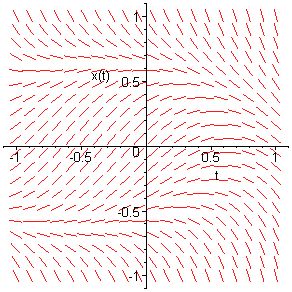
¿Es autónoma la ecuación diferencial? ¿Tiene soluciones no monótonas?
¿constantes? ¿Hay alguna curva solución que sea a la vez curva isoclina?
Solución.-
La ecuación diferencial es autónoma si es de la forma dx/dt=f(x) ;
por lo tanto sus isoclinas deben ser líneas rectas. Si fijamos el valor m
de la pendiente, la isoclina correspondiente es la curva f(x)=m en
el plano de coordenadas (t,x) . Por consiguiente, si el número
c satisface f(c)=m , la recta x=c es parte
de la isoclina de pendiente m.
Así pues, si la ecuación diferencial dada fuese autónoma sus isoclinas
tendrían que ser rectas paralelas al eje horizontal t .
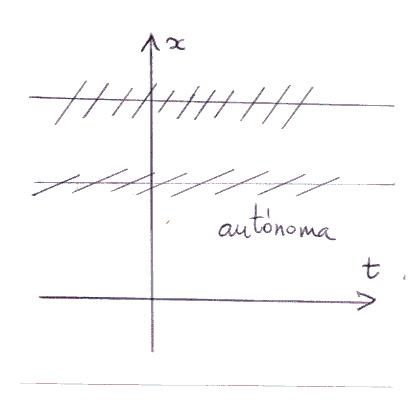
De la
figura se deduce que en este caso las isoclinas no son rectas paralelas
al eje horizontal. Por lo cual, la ecuación dada no es autónoma.
Si consideramos, por ejemplo, la ecuación diferencial autónoma dx/dt=x2 -2 ,
se tiene que la isoclina correspondiente a la pendiente m
es la unión de las dos rectas
x=(2+m)1/2,x=-(2+m)1/2 , siempre que m
sea mayor o igual que -2 .
Hay soluciones que oscilan (o no monótonas). Esta es otra razón
para deducir que la ecuación no es autónoma, pues todas las soluciones
de una ecuación autónoma son monótonas
(crecientes, o decrecientes, o constantes).
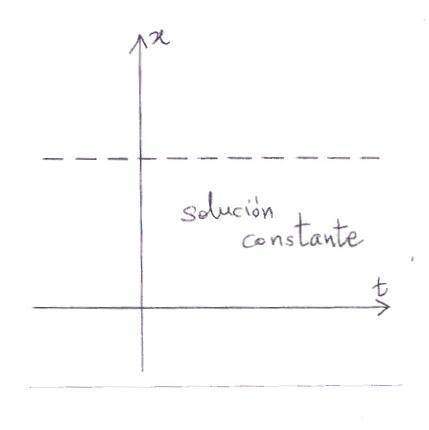
No hay soluciones
constantes pues no se ve una línea recta horizontal en la que las
pendientes sean todas 0; lo que equivale a decir que los segmentitos
deberían estar contenidos en dicha recta. Y esto no ocurre.
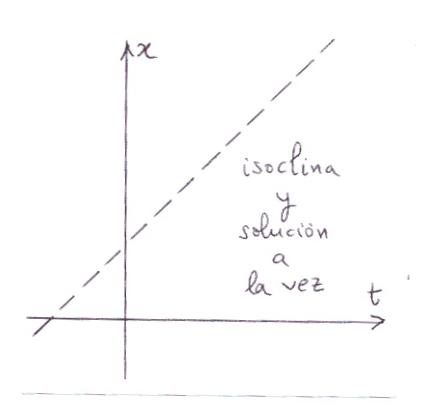
Tampoco hay ninguna isoclina que sea curva solución, pues tendría
que ser una recta (quizás inclinada) y de la figura se deduce que no
existe una recta tal que todos los segmentitos que intercepta estén
contenidos en ella.
Se podrá mirar un resumen se estos hechos en la siguiente imagen
GIF formada por cuatro escenas que se repiten y duran 3 segundos
cada una.
Problema 4


Errores observados al corregir

Alegatos
Portada
de la Sección Departamental
Modificada el 24 de junio de 2006.
Páginas administradas por Juan-Miguel Gracia: