Matemáticas. Capítulo 2. Tema 5 (sigue).
Campos de direcciones. Curvas isoclinas.
1º de Ciencias (CCAA y CTA).
5-33 a 5-57.
Juan-Miguel Gracia
<=== Principio
Siguientes ===>
5-33
5-34
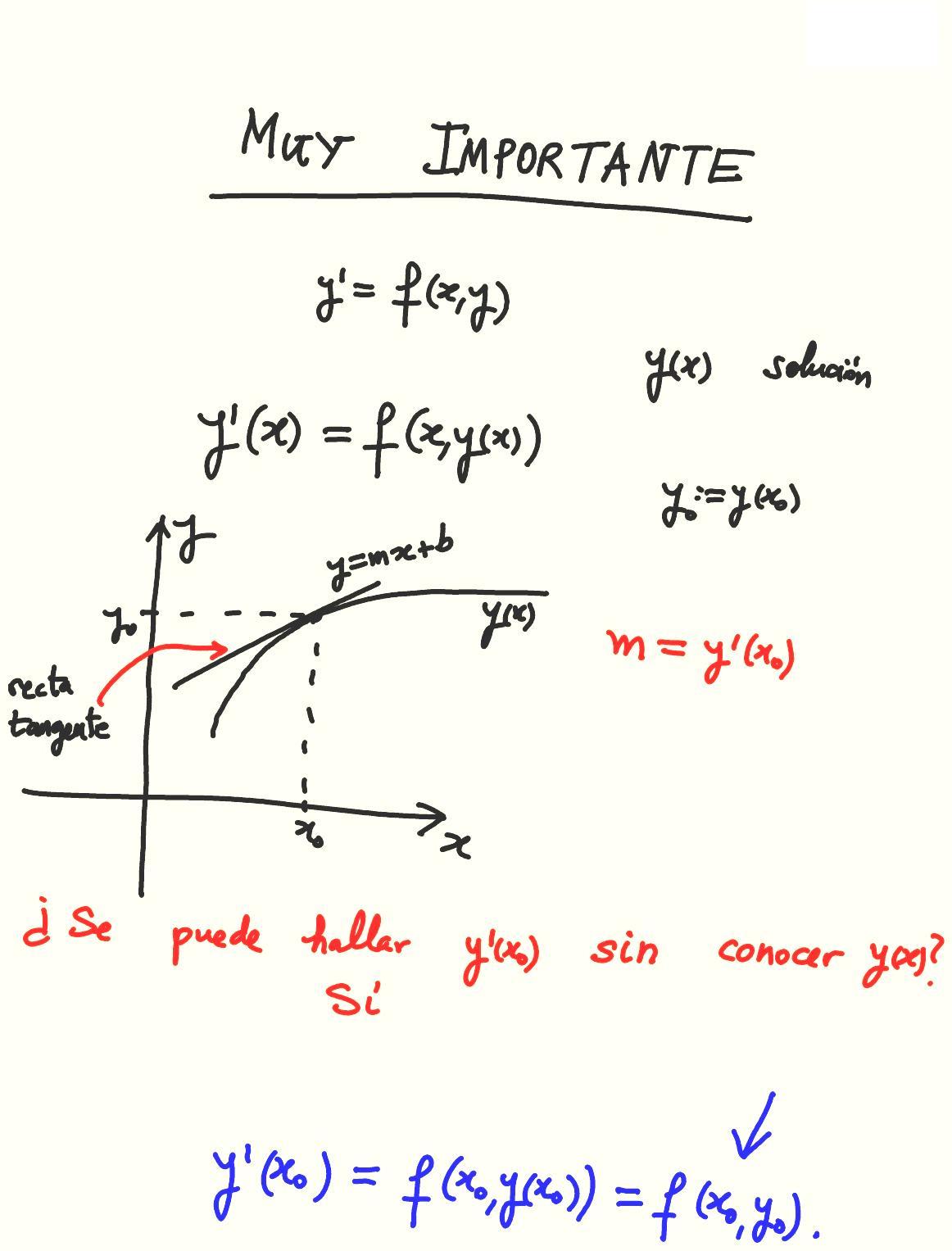

5-35
5-36
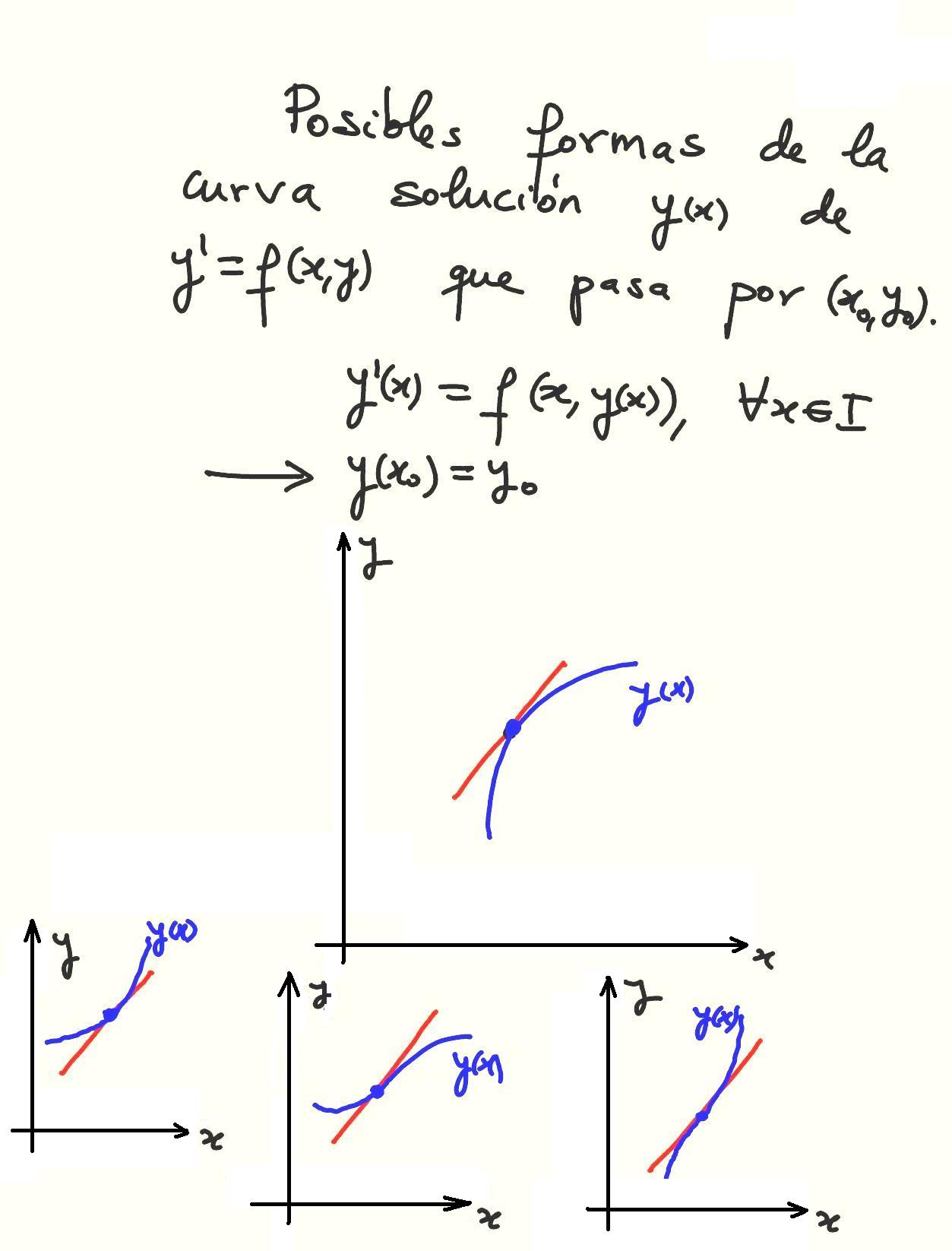
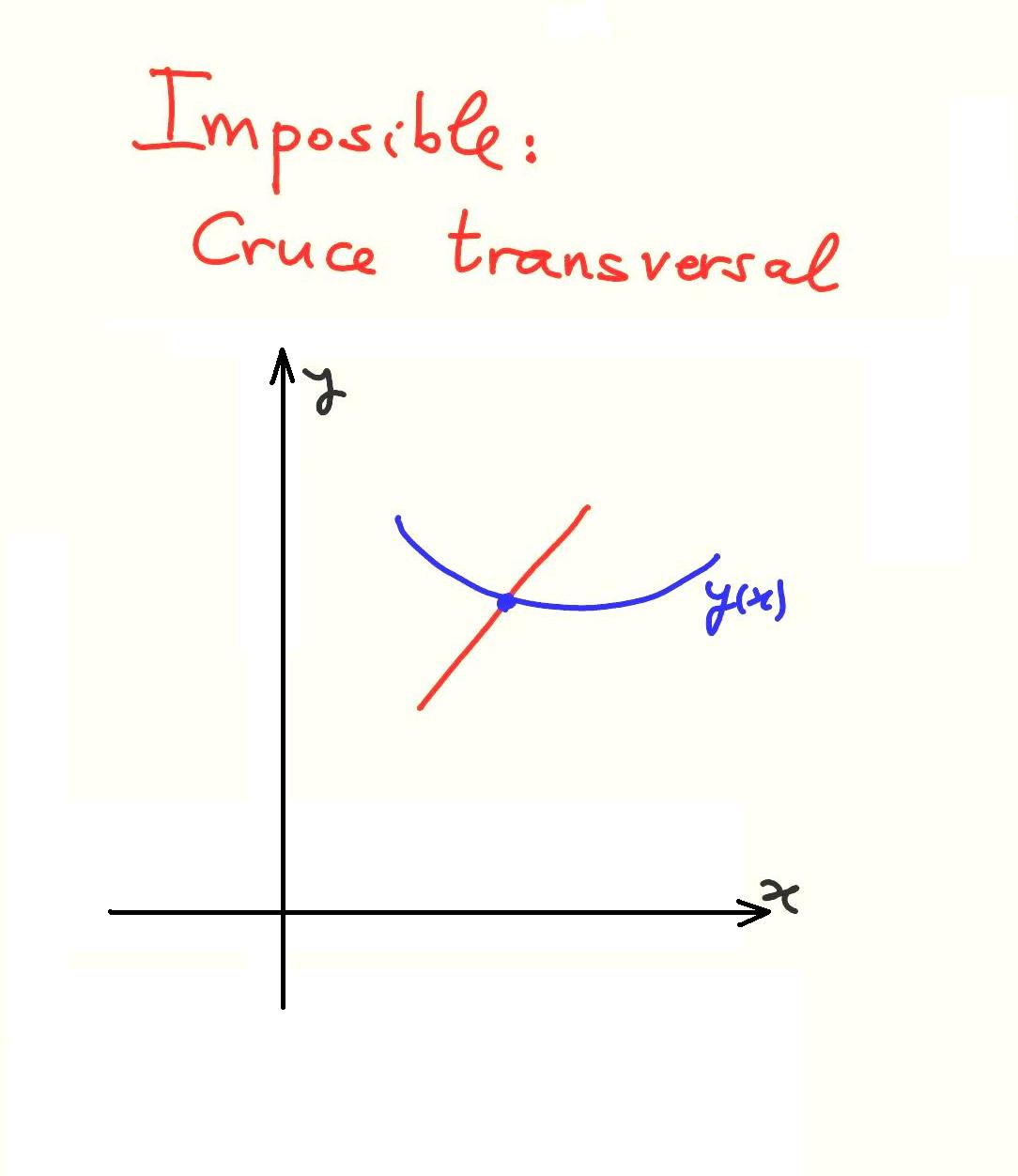
5-37
5-38

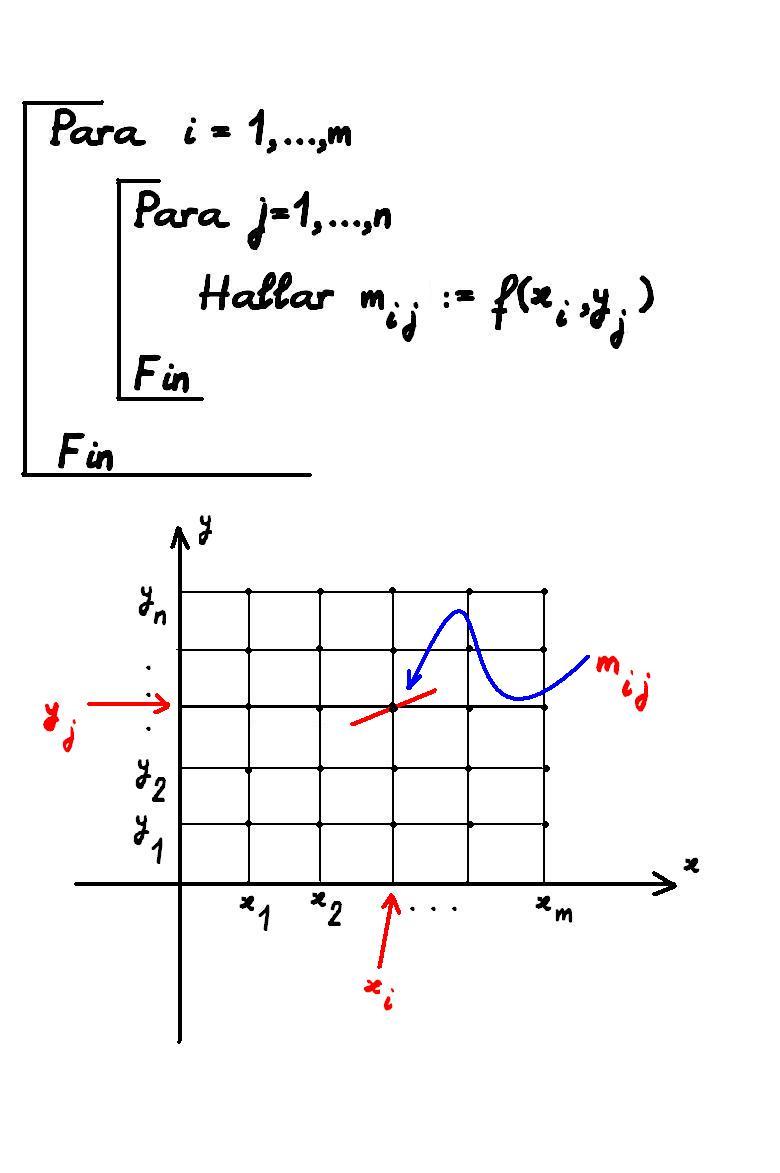
5-39


5-40
5-41
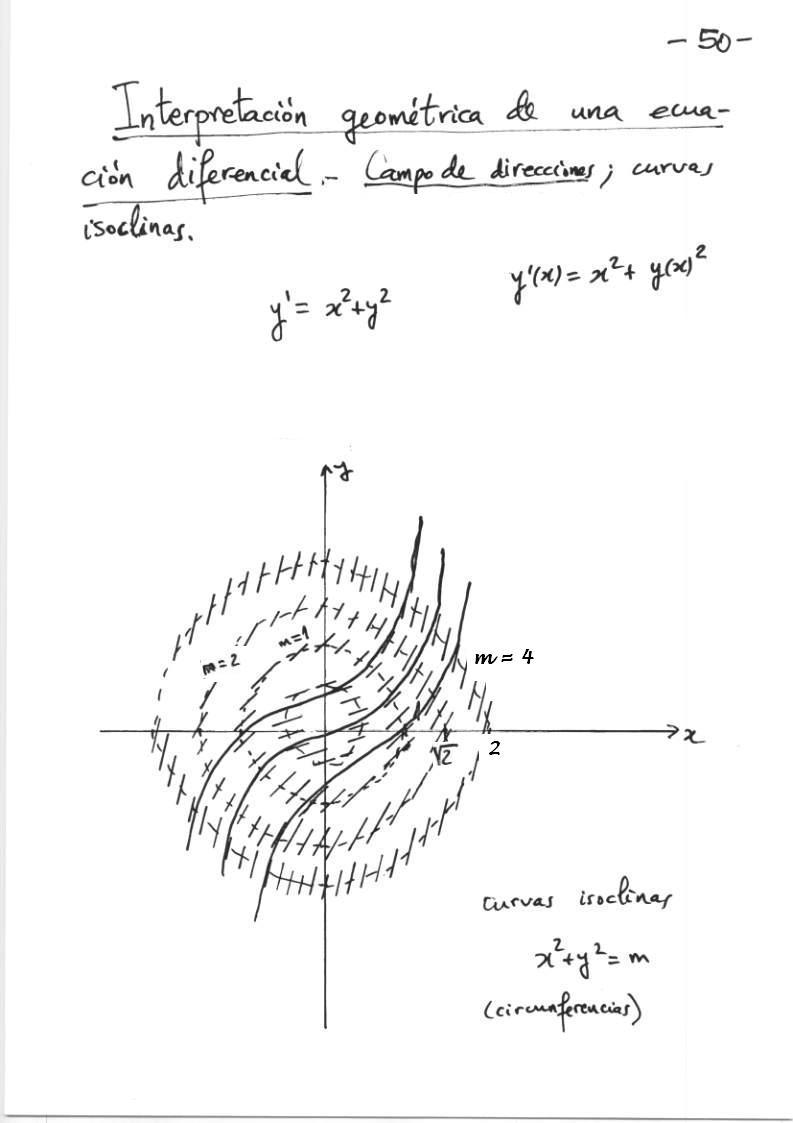
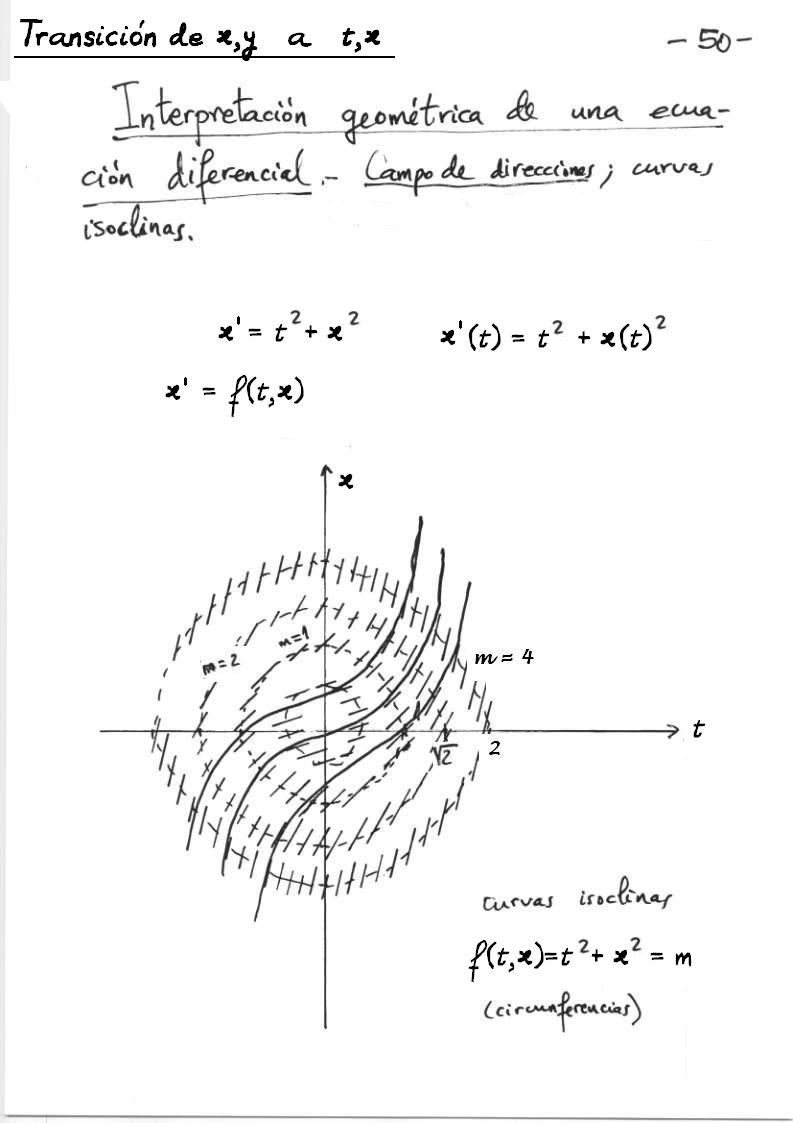
Atención: no es cierto que las
soluciones y(x) de y'=x2+y2 estén definidas para todo valor de
x . Véase una demostración de este aserto aquí.
5-42
5-43
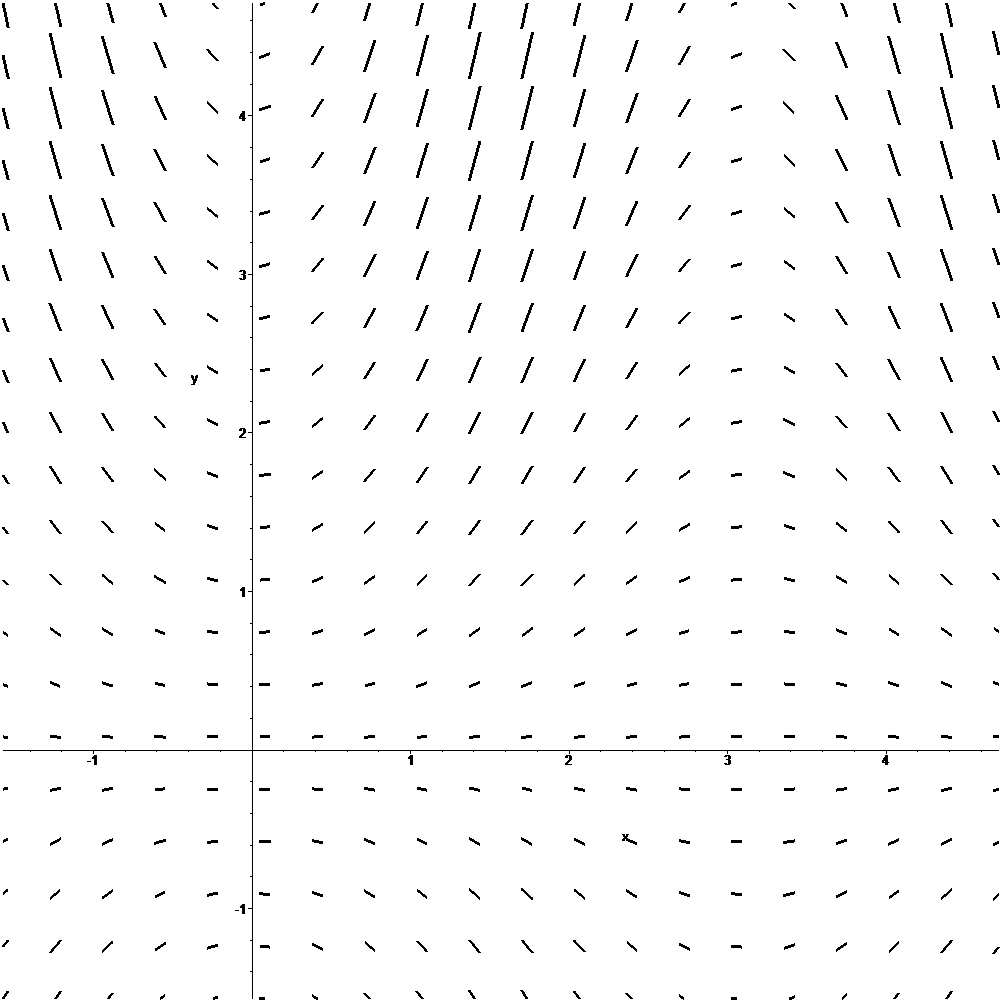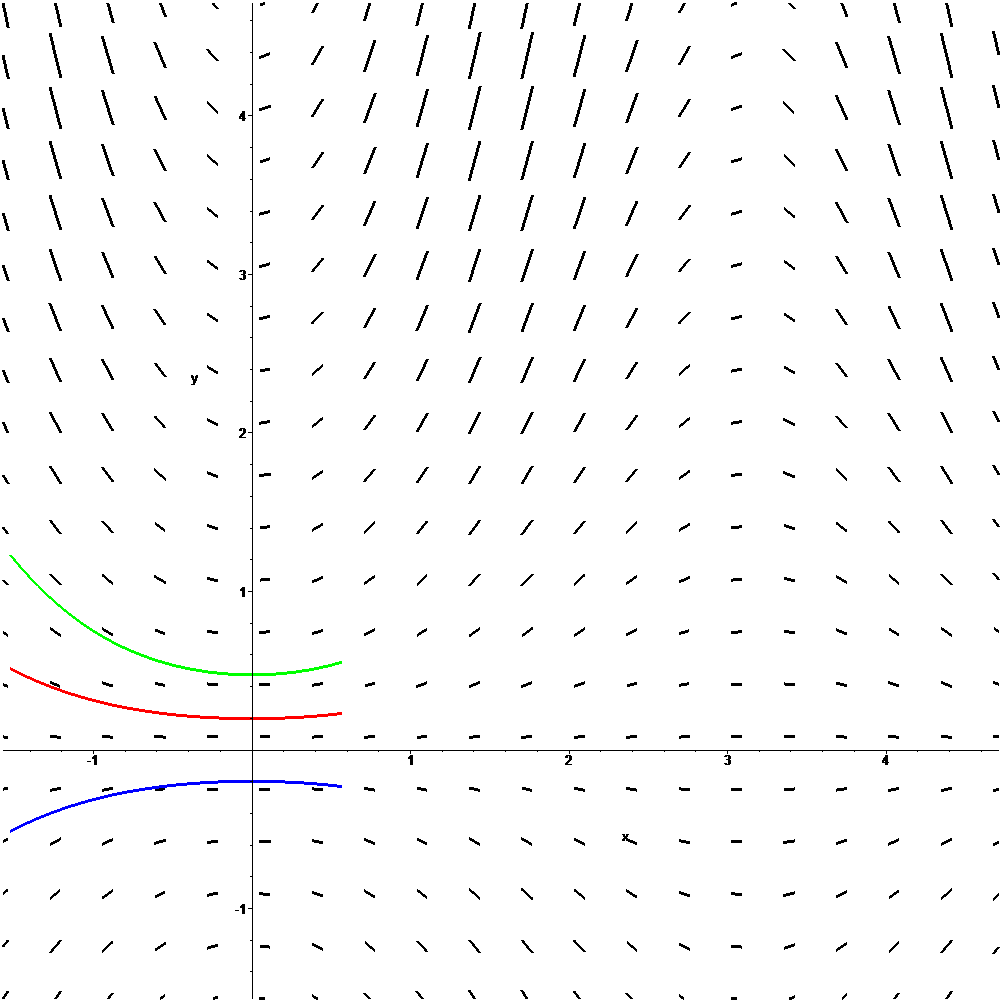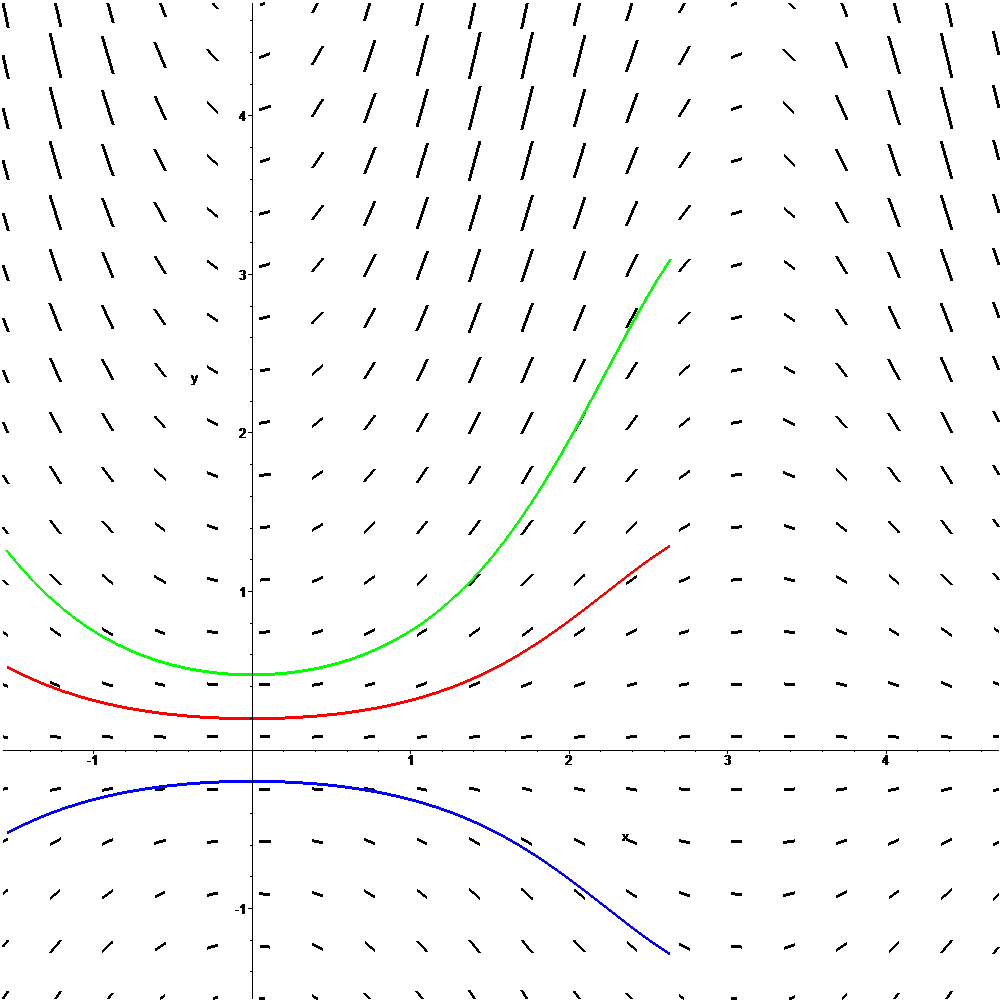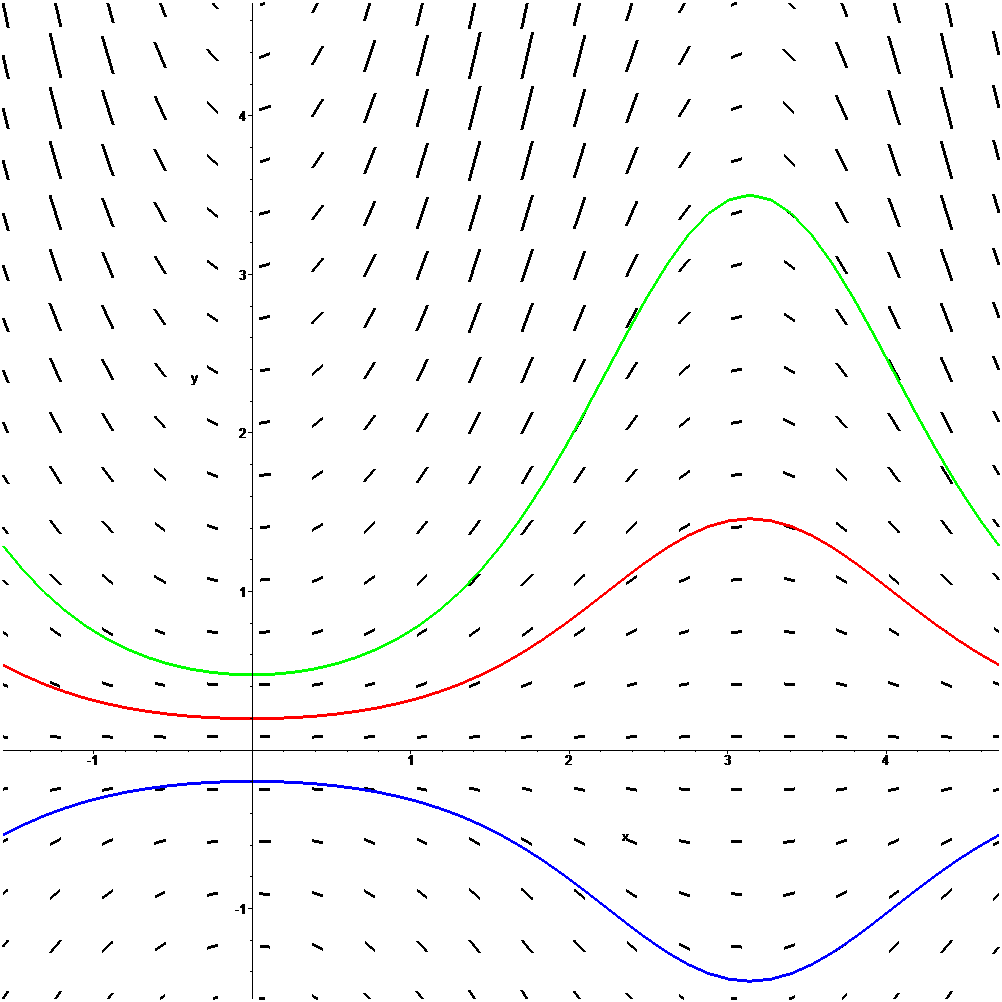
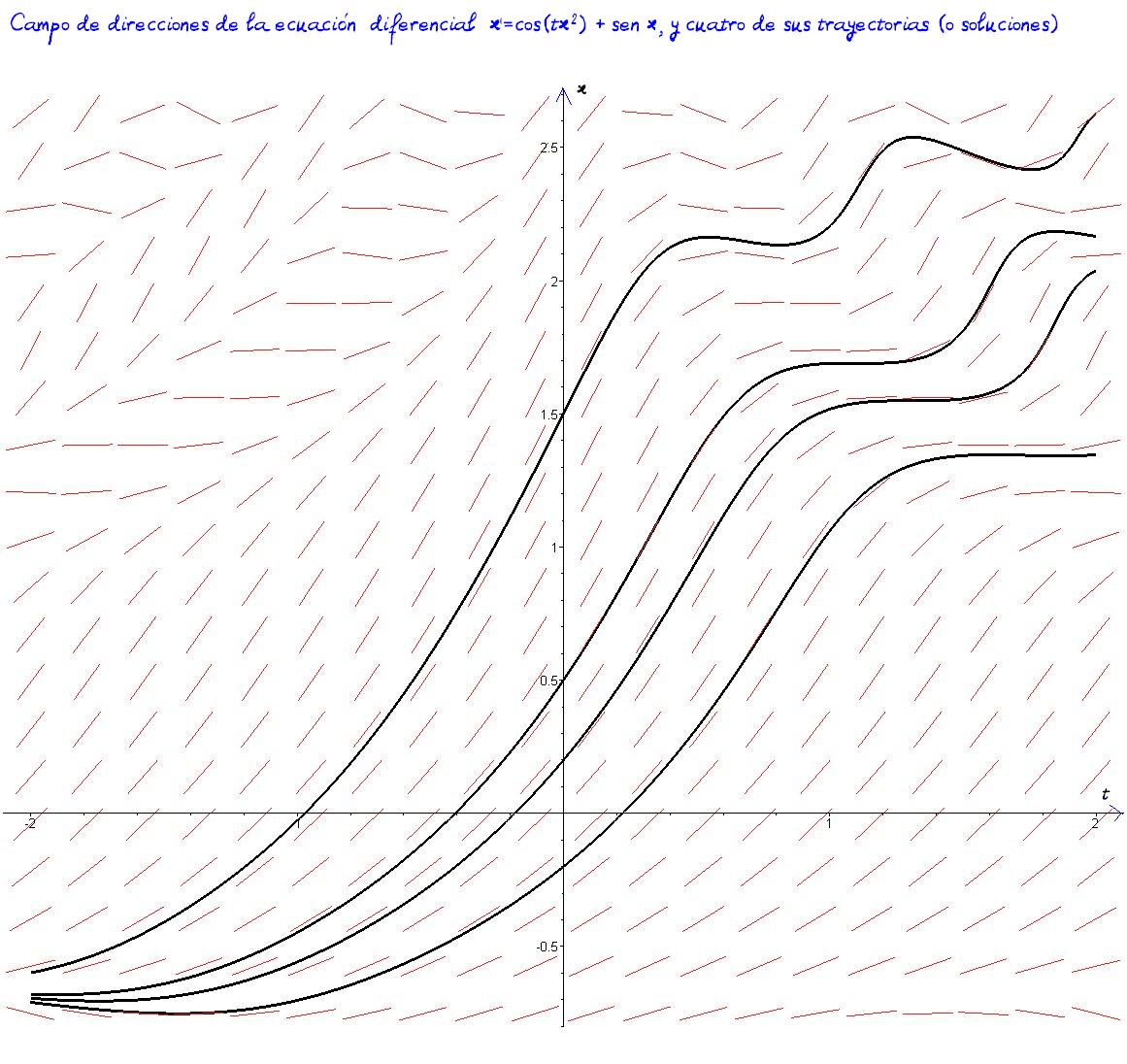
Trayectorias tangentes al campo de pendientes
5-44 5-45
5-46
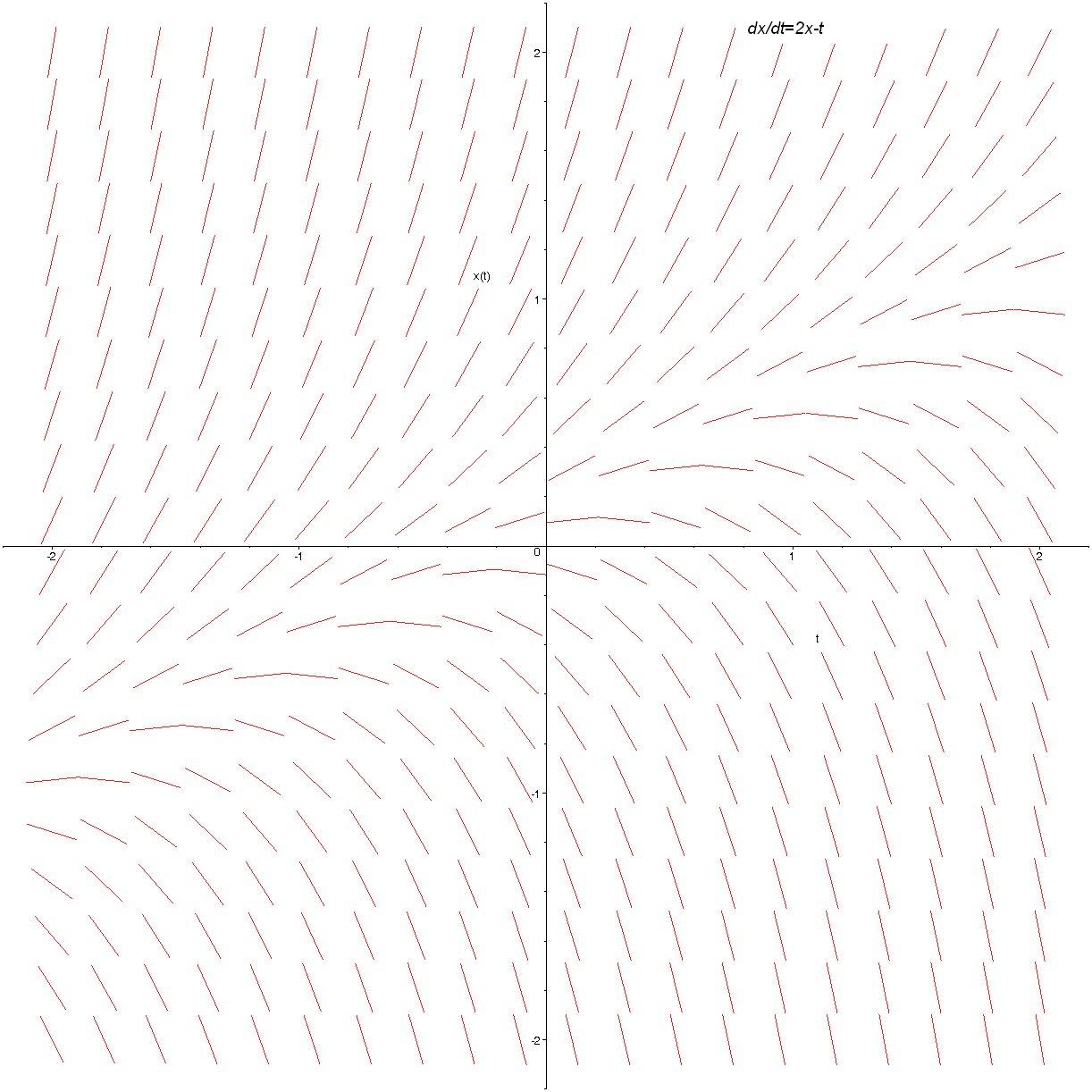
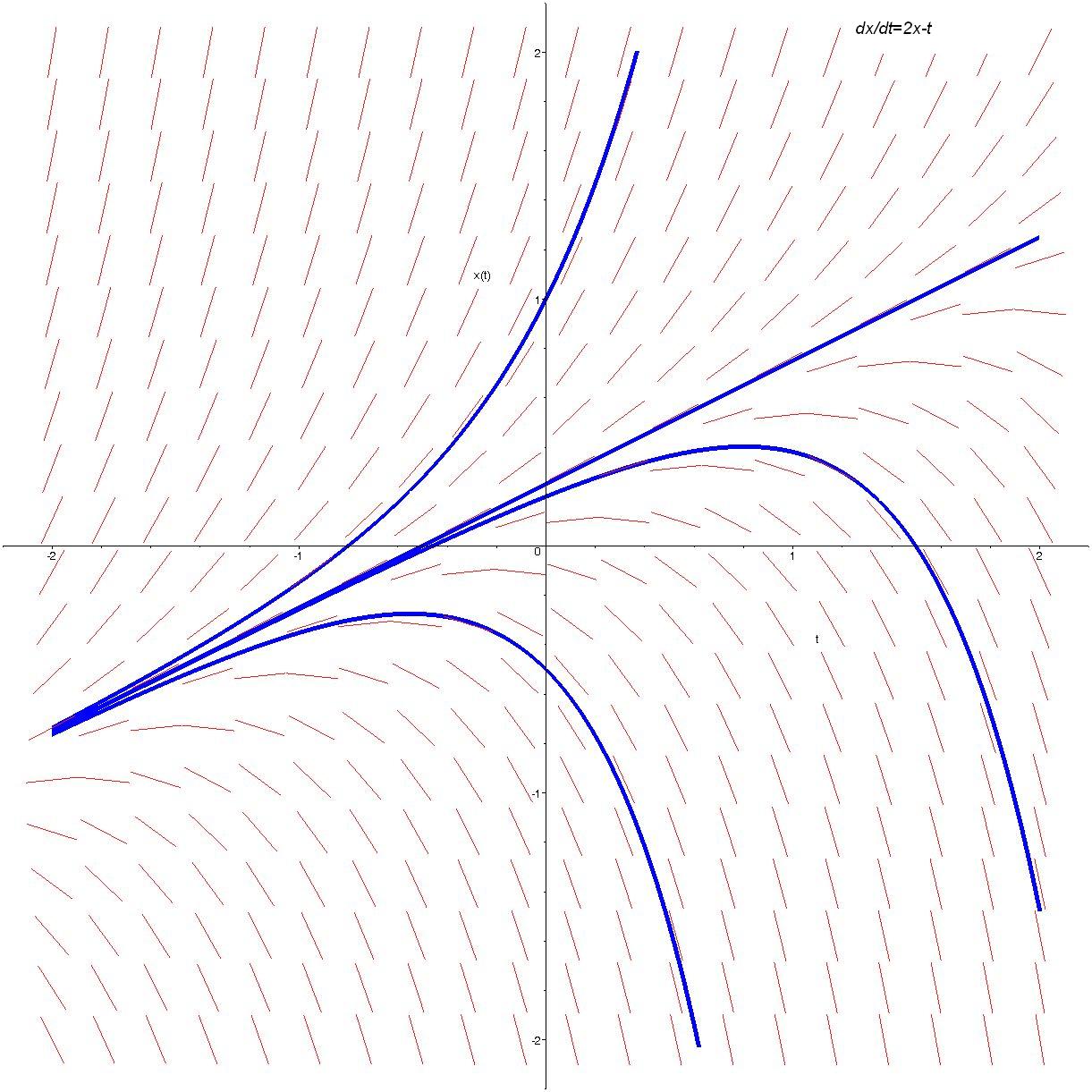

$\textstyle{x'=2x-t}$
5-47 5-48
5-49
.jpg)
_8.jpg)

Trayectorias de la ecuación diferencial autónoma $\textstyle{x'=3x(1-x)}$ en el cuadrado $\textstyle{-2\lt t \lt 2, -2 \lt x \lt 2}$.
5-50
5-51
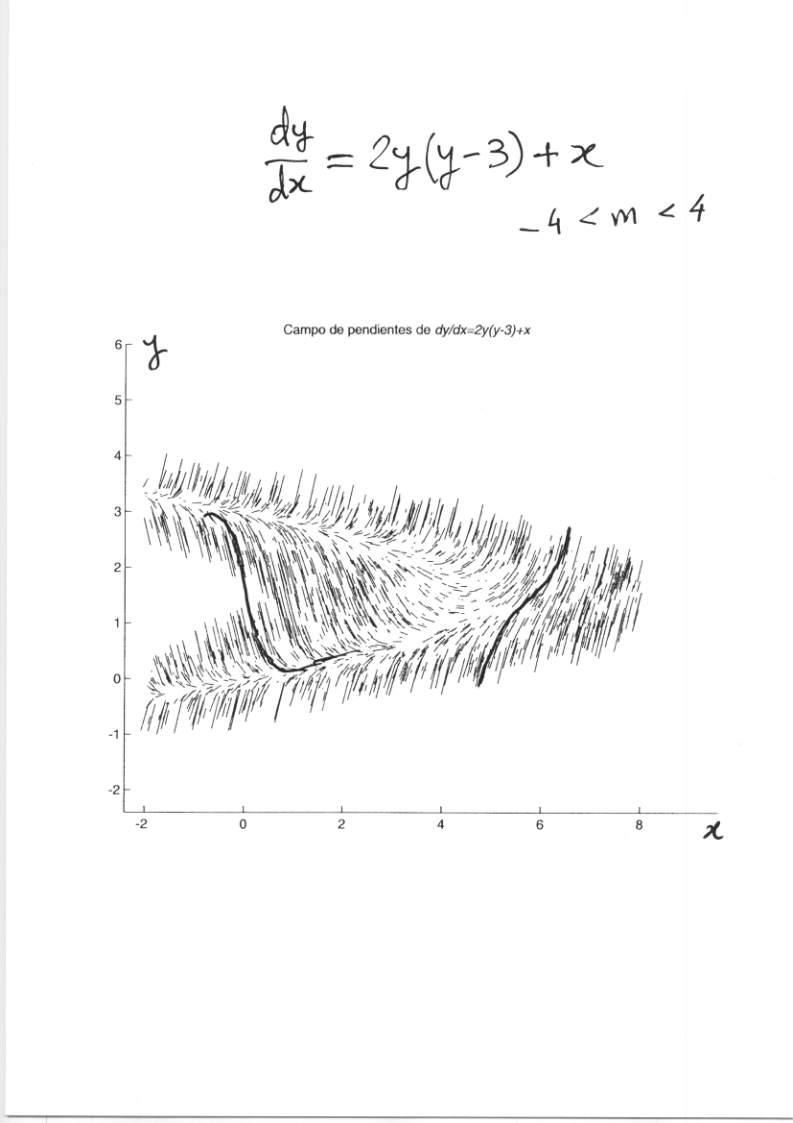
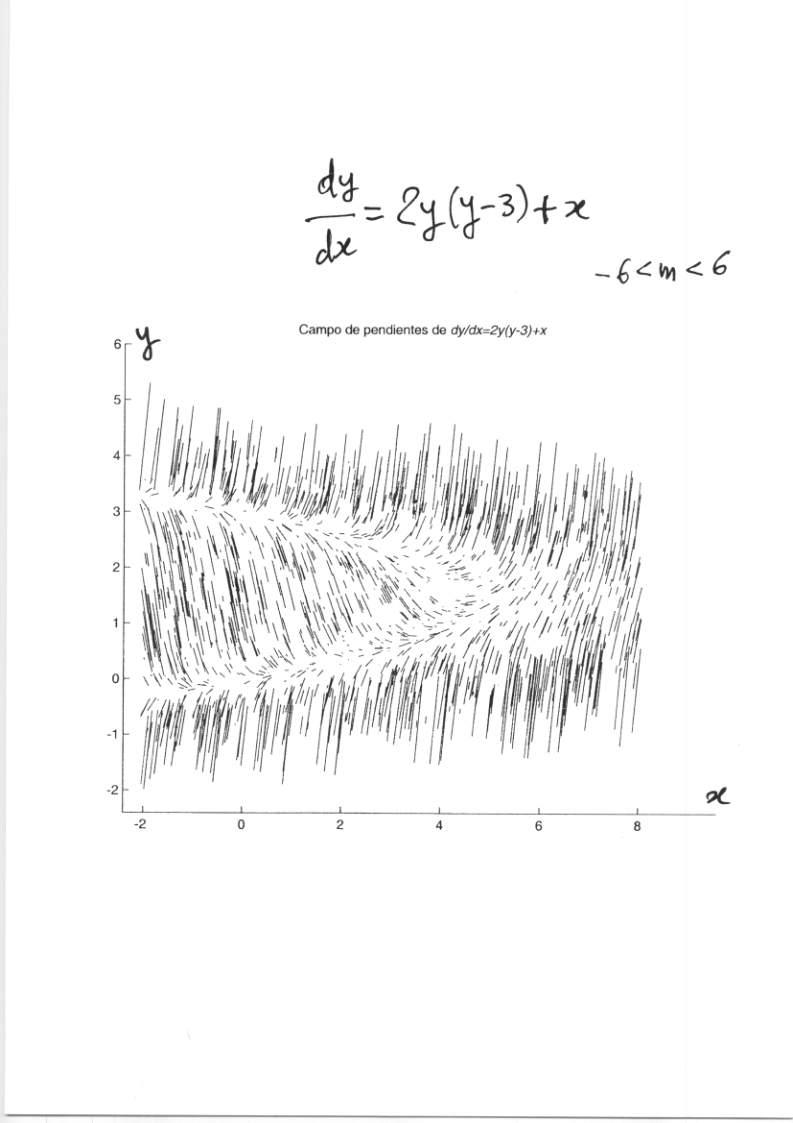
5-52

5-53 5-54
5-55
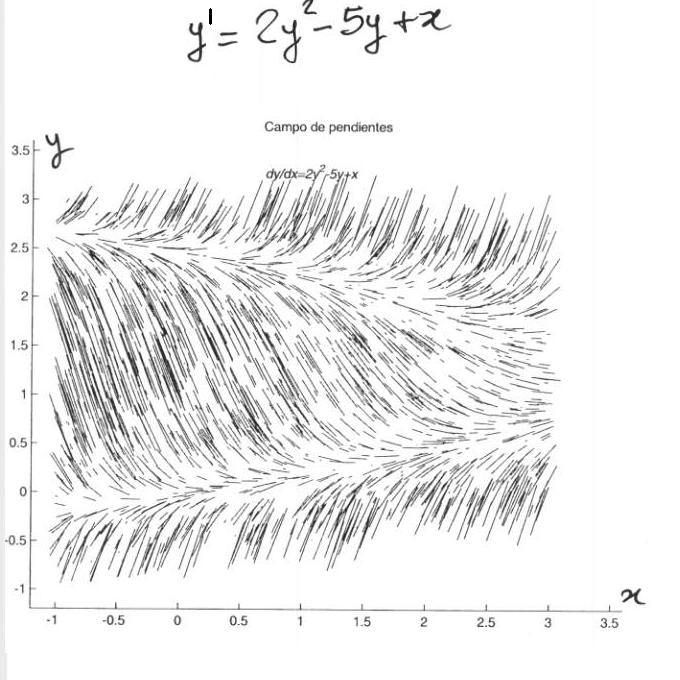


$\textstyle{y'=2y^2-5y+x}$
5-56
5-57
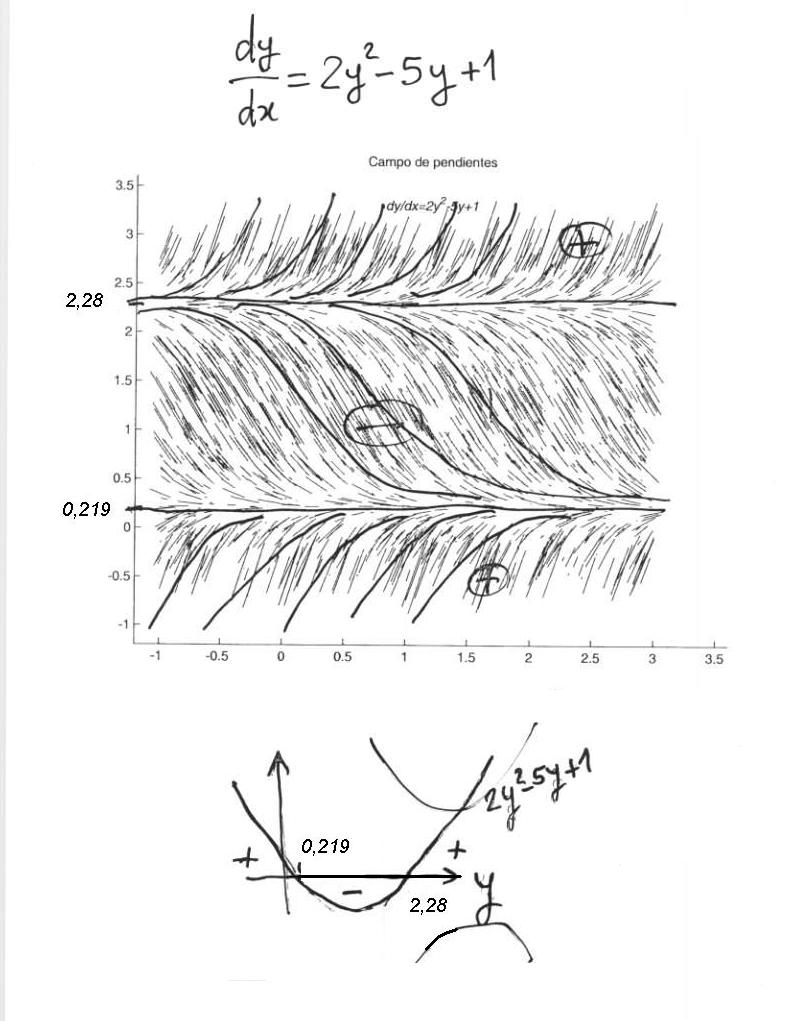

$\textstyle{y'=2y^2-5y+1}$, ecuación diferencial autónoma.
<=== Anteriores
Siguientes
===>
Acreditaciones
- Las películas .mpg y .gif han sido obtenidas con MATLAB con la "toolbox"
vfv para visualizar campos vectoriales, escrita por Nima Bigdely Shamlo.
La he copiado del repositorio de ficheros de terceros en MathWorks.
En particular, he utilizado
la función "explorevfield" que construye una película de MATLAB
o "movie" mediante convolución con integrales curvilíneas ("LIC" o
"Line Integral Convolution"). El método LIC fue ideado por Cabral y Leedom en 1993.
Después he usado la función "movie2avi" de Matlab. Y, finalmente, el fichero "avi2gif.exe"
de VIBROWARE, Ltd.
Portada
de la Sección Departamental
Modificada el 2 de julio de 2013.
Página administrada por Juan-Miguel Gracia:


























.jpg)
_8.jpg)









