Manuscripts from 1996 on
1996
Safety neighbourhoods for the invariants of the matrix
similarity (1996).
Abstract: We give safety
neighbourhoods for the necessary conditions in the change of the
Jordan canonical form of a matrix under small perturbations. We also
obtain the minimum distance from a n × n complex matrix
which has less than k nonconstant invariant factors (k=2,...,n
)
to the set of matrices which have more or equal to k. When
k=2,
we get in particular the distance from a nonderogatory matrix to the set
of derogatory matrices.
rootjord.dvi.
1997
1998
Safety neighbourhoods for the Kronecker canonical form
(1998).
Abstract: We give safety
neighbourhoods for the necessary conditions in the change of the Kronecker
canonical form of a matrix pencil under small perturbations.
root98_2.dvi
Conjectures on pseudospectra, Cassini ovals and Laplacians
(in Spanish) 1998. armonica.dvi.
1999
Smooth Jordanization (1999).
Abstract: Let A be
a square complex matrix function of class Cp defined
on an open interval (a,b) of the real line. Then for all t in
(a,b),
the matrix A(t) is similar to a matrix Jt
in Jordan
form; so there exists an invertible matrix Pt
such that
Pt-1A(t)Pt=Jt. We give
a partial answer to the question: Can the function that associates
Pt
with t be chosen of class Cp?
smojorda.ps.
Nearest pair with more nonconstant invariant factors.
Pseudospectrum (1999).
Abstract: Let (A,B) be a
pair of complex matrices n × n y n × m. Suppose that the number
of nonconstant (¹ 1) invariant factors
of the polynomial matrix l[In,0]-[A,B]
is less than k . For all complex number l denote
by sn-(k-1) (l[In,0]-[A,B]
) the greatest (n-(k-1))th singular value of the matrix l[In,0]-[A,B].
The minimum absolute value of the real function of a complex variable l
® sn-(k-1) (l[In,0]-[A,B]
) gives the distance from (A,B) to the set of pairs with more or equal
number of nonconstant invariant factors. When k=1, this specializes in
the formula of Eising for the distance from a controllable pair (A,B) to
the nearest uncontrollable pair.
The complex numbers l
lying
in the subset level { l Î C :
sn (l[In,0]-[A,B]
) £ e } are the uncontrollable modes of
all the pairs that are within an e tolerance
of (A,B).
uno99.dvi
Flows of matrix pencils (April 21, 1999).
Abstract: We consider some matrix ordinary
differential equations whose solutions preserve some features of the initial
conditions; for example the Kronecker canonical form of a matrix pencil,
or the Brunovsky canonical form of a matrix pair.
flows.dvi
2000
2001
Geometric multiplicity margin for a submatrix
(February 19, 2001).
Abstract: Let G be
a square complex matrix with less than k nonconstant invariant factors.
We find a complex matrix that gives an optimal approximation to G
among all possible matrices that have more than or equal to k invariant
factors, obtained by varying only the entries of a bottom right submatrix
of G.
Paper: margin.dvi,
margin.ps,
margin.pdf
Screen: marginweb.pdf.
The multiplicative integral (in Spanish) October 21,
2001.
Abstract: It is analyzed the relation of
the multiplicative integral of Volterra with the logarithmic derivative
and the linear differential systems.
Screen: InteMult.pdf.
2002
xyz (in Spanish) January 21, 2002
.
Abstract: The key importance
of the symbols for the comprehension of the mathematics is emphasized that,
without them, they would be unintelligible. The evolution is analyzed of
some of these signs. Likewise, the great utility is commented of the notation
of Leibniz for the teaching of the infinitesimal calculus.
Screen:
xyz.pdf.
Paper: xyzp.pdf.
Source: xyz.tex.
Linear algebra behind the search engines of Internet
(in Spanish) November 11, 2002.
Abstract: There are analyzed
two applications of linear algebra to the search engines of Internet: the
value assigned to every web page by Google (PageRank), and the latent semantic
analysis.
Screen: busca.pdf.
Paper: buscap.pdf.
If you have trouble to see the
links that appear in busca.pdf, download the file defi.pdf,
and put both files in the same folder.
Nonnegative matrices, random walks and Markov chains
(in Spanish) November 11, 2002.
Abstract: We give some definitions
of digraph, Markov chain, random walk, as well as its relation with the
theory of Perron Frobenius of nonnegative matrices. It contains programs
in Matlab.
Screen: defi.pdf.
Paper: defip.pdf.
2003
2004
Multiplicities of pseudoeigenvalues, Presentation
ILAS04, Coimbra, July 20, 2004.
Abstract: Let A be an n-by-n complex matrix. For each ε >
0 let T be a connected component of the strict ε-pseudospectrum of A.
The sum of the algebraic multiplicities of the eigenvalues of all matrices X such
that || X - A || < ε that are inside T, is equal to the sum of
the algebraic multiplicities of all eigenvalues that are inside T. Here ||·|| is the
spectral norm.
Screen: multpseudo.pdf.
Alternative files for screen:
mltpsd.pdf; +
figures.pdf; or pvisible.pdf
Concept of pseudospectra
The pseudospectrum of an n-by-n complex matrix A, of level
ε > 0 , is defined as the union of all spectra of the matrices X
that are in the closed ball centered at A and radius ε in the
matrix space, where the distance in this space is the one associated to the spectral norm.
It is noted by Λε (A).
Next you can see an animated gif image that show the evolution of
Λε (A)
when ε increases from 0.

This animation belongs to the matrix of order 3
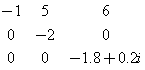
whose eigenvalues are
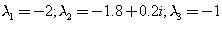
The condition numbers of these (simple) eigenvalues are, respectively,
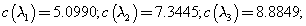
The three connected components of the level ε pseudospectrum
grow so much more quickly the more big is the condition number of the eigenvalue
of A that contain.
In fact, if δj(ε) is the
diameter of the connected component that contains the j-th eigenvalue, then its right
derivative at 0 satisfies
δ'j(0+)= 2 c(λj).
More information about pseudospectra of a matrix can
be seen in

2005
Nearest matrix with two prescribed eigenvalues,
link to the journal Linear Algebra and Its Applications.
2006
Stability of controlled invariant subspaces, with Francisco E. Velasco:
link to the journal Linear Algebra and Its Applications.
2008
Nearest southeast submatrix that makes multiple a prescribed eigenvalue. Part 1, jointly with Francisco E. Velasco:
link to the journal Linear Algebra and Its Applications.
2009
Multiplicities of the structured pseudoeigenvalues. arXiv:0907.1980v2 [math.SP]
Limits of the singular values of a pencil of matrices, (in Spanish) Limites.pdf
(talk).
2010
Nearest southeast submatrix that makes multiple an eigenvalue of the normal northwest submatrix,
pdf , jointly with Francisco E. Velasco
Lipschitz stability of controlled invariant subspaces,
pdf , jointly with Francisco E. Velasco
Identical pseudospectra of any geometric multiplicity,
pdf, jointly with Gorka Armentia and Francisco E. Velasco
Derivatives of the diameter and the area of a connected component of the pseudospectra,
pdf, jointly with Gorka Armentia and Francisco E. Velasco
Second order pseudospectra of normal matrices,
pdf, jointly with Gorka Armentia and Francisco E. Velasco
2014
My road to the spectral perturbation of matrices, pdf.
Beamer presentation that contains my goodbye talk in the congress ALAMA-GAMM/ANLA'2014, July 14-16, Barcelona, Spain, dedicated to homage to me, Juan-Miguel Gracia,
with ocassion of my retirement in 2015.
Also you can be here an Spanish excerpt of what I said in that conference.
Books that every student of Mathematics should read
-
Z.A. Melzak: Companion to Concrete Mathematics, Edit. Wiley, New
York, 1973.
-
Z.A. Melzak: Mathematical Ideas, Modeling and Applications, Edit.
Wiley, New York, 1976.
Last update: April 23, 2022.